Stacks And Queues

Stacks and queues: Stacks and queues are dynamic sets in which the element removed from the set by the DELETE operation is prespecified. In a stack, the element deleted from the set is the one most recently inserted: the stack implements a last-in, first-out, or LIFO, policy. Similarly, in a queue, the element deleted is always the one that has been in the set for the longest time: the queue implements a first-in, first out, or FIFO, policy. There are several efficient ways to implement stacks and queues on a computer. In this section we show how to use a simple array to implement each.

Stacks: The INSERT operation on a stack is often called PUSH, and the DELETE operation, which does not take an element argument, is often called POP. These names are allusions to physical stacks, such as the spring-loaded stacks of plates used in cafeterias. The order in which plates are popped from the stack is the reverse of the order in which they were pushed onto the stack, since only the top plate is accessible.

As shown in Figure 10.1, we can implement a stack of at most n elements with an array S[1, ‥ n]. The array has an attribute top[S] that indexes the most recently inserted element. The stack consists of elements S[1 ‥ top[S]], where S[1] is the element at the bottom of the stack and S[top[S]] is the element at the top.

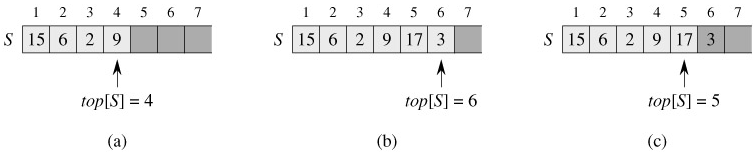
Figure 10.1: An array implementation of a stack S. Stack elements appear only in the lightly shaded positions. (a) Stack S has 4 elements. The top element is 9. (b) Stack S after the calls PUSH(S, 17) and PUSH(S, 3). (c) Stack S after the call POP(S) has returned the element 3, which is the one most recently pushed. Although element 3 still appears in the array, it is no longer in the stack; the top is element 17.

When top[S] = 0, the stack contains no elements and is empty. The stack can be tested for emptiness by the query operation STACK-EMPTY. If an empty stack is popped, we say the stack underflows, which is normally an error. If top[S] exceeds n, the stack overflows. (In our pseudocode implementation, we don't worry about stack overflow.)

The stack operations can each be implemented with a few lines of code.

			STACK-EMPTY(S)
1  if top[S] = 0
2      then return TRUE
3      else return FALSE

PUSH(S, x)
1  top[S] ← top[S]   1
2  S[top[S]] ← x

POP(S)
1  if STACK-EMPTY(S)
2     then error "underflow"
3     else top[S] ← top[S] - 1
4          return S[top[S]   1]

Figure 10.1 shows the effects of the modifying operations PUSH and POP. Each of the three stack operations takes O(1) time.

Queues

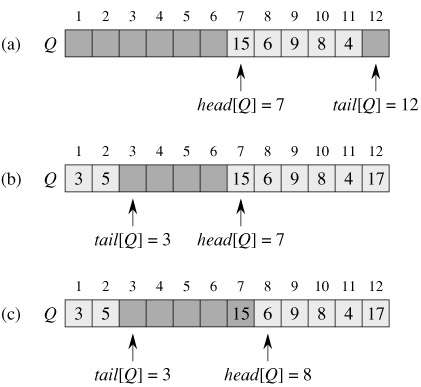
We call the INSERT operation on a queue ENQUEUE, and we call the DELETE operation DEQUEUE; like the stack operation POP, DEQUEUE takes no element argument. The FIFO property of a queue causes it to operate like a line of people in the registrar's office. The queue has a head and a tail. When an element is enqueued, it takes its place at the tail of the queue, just as a newly arriving student takes a place at the end of the line. The element dequeued is always the one at the head of the queue, like the student at the head of the line who has waited the longest. (Fortunately, we don't have to worry about computational elements cutting into line.)

Figure 10.2 shows one way to implement a queue of at most n - 1 elements using an array Q[1 ‥ n]. The queue has an attribute head[Q] that indexes, or points to, its head. The attribute tail[Q] indexes the next location at which a newly arriving element will be inserted into the queue. The elements in the queue are in locations head[Q], head[Q] 1,..., tail[Q] - 1, where we "wrap around" in the sense that location 1 immediately follows location n in a circular order. When head[Q] = tail[Q], the queue is empty. Initially, we have head[Q] = tail[Q] = 1. When the queue is empty, an attempt to dequeue an element causes the queue to underflow. When head[Q] = tail[Q] 1, the queue is full, and an attempt to enqueue an element causes the queue to overflow.