Standard Notations And Common Functions

Standard notations and common functions: This section reviews some standard mathematical functions and notations and explores the relationships among them. It also illustrates the use of the asymptotic notations.

Monotonicity: A function f(n) is monotonically increasing if m ≤ n implies f(m) ≤ f(n). Similarly, it is monotonically decreasing if m ≤ n implies f(m) ≥ f(n). A function f(n) is strictly increasing if m < n implies f(m) < f(n) and strictly decreasing if m < n implies f(m) > f(n).

Floors and ceilings: For any real number x, we denote the greatest integer less than or equal to x by ⌊x⌋(read "the floor of x") and the least integer greater than or equal to x by ⌈x⌉(read "the ceiling of x"). For all real x,

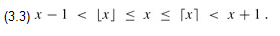
For any integer n,

⌈n/2⌉ ⌊n/2⌋ = n,

and for any real number n ≥ 0 and integers a, b > 0,

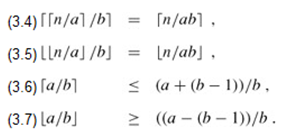
The floor function f(x) = ⌊x⌋ is monotonically increasing, as is the ceiling function f(x) = ⌈x⌉.

Modular arithmetic: For any integer a and any positive integer n, the value a mod n is the remainder(or residue) of the quotient a/n:

Given a well-defined notion of the remainder of one integer when divided by another, it is convenient to provide special notation to indicate equality of remainders. If (a mod n) = (b mod n), we write a ≡ b (mod n) and say that a is equivalent to b, modulo n. In other words, a ≡ b (mod n) if a and b have the same remainder when divided by n. Equivalently, a ≡ b (mod n) if and only if n is a divisor of b - a. We write a ≢ b (mod n) if a is not equivalent to b, modulo n.

Polynomials: Given a nonnegative integer d, a polynomial in n of degree dis a function p(n) of the form

Where the constants a₀, a₁, ..., a_d are the coefficients of the polynomial and a_d ≠ 0. A polynomial is asymptotically positive if and only if a_d > 0. For an asymptotically positive polynomial p(n) of degree d, we have p(n) = Θ(n^d). For any real constant a ≥ 0, the function n^a is monotonically increasing, and for any real constant a ≤ 0, the function n^a is monotonically decreasing. We say that a function f(n) is polynomially bounded if f(n) = O(n^k) for some constant k.