String Matching
Overview
Finding all occurrences of a pattern in a text is a problem that arises frequently in text-editing programs. Typically, the text is a document being edited, and the pattern searched for is a particular word supplied by the user. Efficient algorithms for this problem can greatly aid the responsiveness of the text-editing program. String-matching algorithms are also used, for example, to search for particular patterns in DNA sequences.
We formalize the string-matching problem as follows. We assume that the text is an array T [1 ‥ n] of length n and that the pattern is an array P[1 ‥ m] of length m ≤ n. We further assume that the elements of P and T are characters drawn from a finite alphabet Σ. For example, we may have Σ = {0, 1} or Σ = {a, b, . . . , z}. The character arrays P and T are often called strings of characters.
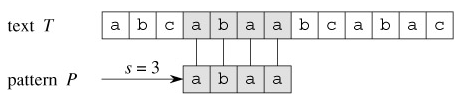
We say that pattern P occurs with shift s in text T (or, equivalently, that pattern P occurs beginning at position s 1 in text T) if 0 ≤ s ≤ n - m and T [s 1 ‥ s m] = P[1 ‥ m] (that is, if T [s j] = P[ j], for 1 ≤ j ≤ m). If P occurs with shift s in T , then we call s a valid shift; otherwise, we call s an invalid shift. The string-matching problem is the problem of finding all valid shifts with which a given pattern P occurs in a given text T . Figure 32.1 illustrates these definitions.
Except for the naive brute-force algorithm, which we review in The naive string-matching algorithm, each string-matching algorithm in this chapter performs some preprocessing based on the pattern and then finds all valid shifts; we will call this latter phase "matching." Figure 32.2 shows the preprocessing and matching times for each of the algorithms in this chapter. The total running time of each algorithm is the sum of the preprocessing and matching times. The Rabin-Karp algorithm presents an interesting string-matching algorithm, due to Rabin and Karp. Although the Θ((n - m 1)m) worst-case running time of this algorithm is no better than that of the naive method, it works much better on average and in practice. It also generalizes nicely to other pattern-matching problems. String matching with finite automata then describes a string-matching algorithm that begins by constructing a finite automaton specifically designed to search for occurrences of the given pattern P in a text. This algorithm takes O(m |Σ|) preprocessing time but only Θ(n) matching time. The similar but much cleverer Knuth-Morris-Pratt (or KMP) algorithm is presented in The Knuth-Morris-Pratt algorithm; the KMP algorithm has the same Θ(n) matching time, and it reduces the preprocessing time to only Θ(m).
|
Algorithm |
Preprocessing time |
Matching time |
|---|---|---|
|
|
||
|
Naive |
0 |
O((n - m 1)m) |
|
Rabin-Karp |
Θ(m) |
O((n - m 1)m) |
|
Finite automaton |
O(m |Σ|) |
Θ(n) |
|
Knuth-Morris-Pratt |
Θ(m) |
Θ(n) |
Figure 32.2: The string-matching algorithms in this chapter and their preprocessing and matching times.
Notation and terminology
We shall let Σ* (read "sigma-star") denote the set of all finite-length strings formed using characters from the alphabet Σ. In this chapter, we consider only finite-length strings. The zero-length empty string, denoted ε, also belongs to Σ*. The length of a string x is denoted |x|. The concatenation of two strings x and y, denoted xy, has length |x| |y| and consists of the characters from x followed by the characters from y.
We say that a string w is a prefix of a string x, denoted w ⊏ x, if x = wy for some string y ∈ Σ*. Note that if w ⊏ x, then |w| ≤ |x|. Similarly, we say that a string w is a suffix of a string x, denoted w ⊐ x, if x = yw for some y ∈ Σ*. It follows from w ⊐ x that |w| ≤ |x|. The empty string ε is both a suffix and a prefix of every string. For example, we have ab ⊏ abcca and cca ⊐ abcca. It is useful to note that for any strings x and y and any character a, we have x ⊐ y if and only if xa ⊐ ya. Also note that ⊏ and ⊐ are transitive relations.