Strongly Connected Components

Strongly connected components: We now consider a classic application of depth-first search: decomposing a directed graph into its strongly connected components. This section shows how to do this decomposition using two depth-first searches. Many algorithms that work with directed graphs begin with such a decomposition. After decomposition, the algorithm is run separately on each strongly connected component. The solutions are then combined according to the structure of connections between components.

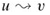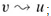A strongly connected component of a directed graph G = (V, E) is a maximal set of vertices C ⊆ V such that for every pair of vertices u and v in C, we have both and ; that is, vertices u and v are reachable from each other. Figure 22.9 shows an example.

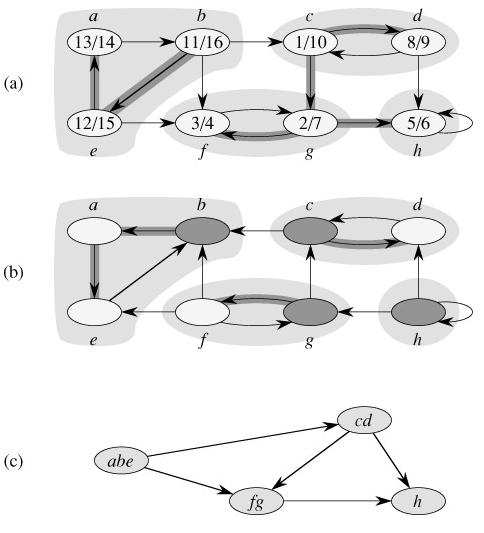
Figure 22.9: (a) A directed graph G. The strongly connected components of G are shown as shaded regions. Each vertex is labeled with its discovery and finishing times. Tree edges are shaded. (b) The graph G^T, the transpose of G. The depth-first forest computed in line 3 of STRONGLY-CONNECTED-COMPONENTS is shown, with tree edges shaded. Each strongly connected component corresponds to one depth-first tree. Vertices b, c, g, and h, which are heavily shaded, are the roots of the depth-first trees produced by the depth-first search of G^T. (c) The acyclic component graph G^SCC obtained by contracting all edges within each strongly connected component of G so that only a single vertex remains in each component.

Our algorithm for finding strongly connected components of a graph G = (V, E) uses the transpose of G. Given an adjacency-list representation of G, the time to create G^T is O(V E). It is interesting to observe that G and G^T have exactly the same strongly connected components: u and v are reachable from each other in G if and only if they are reachable from each other in G^T. Figure 22.9(b) shows the transpose of the graph in Figure 22.9(a), with the strongly connected components shaded.

The following linear-time (i.e., Θ(V E)-time) algorithm computes the strongly connected components of a directed graph G = (V, E) using two depth-first searches, one on G and one on G^T.

	STRONGLY-CONNECTED-COMPONENTS (G)
1  call DFS (G) to compute finishing times f[u] for each vertex u
2  compute GT
3  call DFS (GT), but in the main loop of DFS, consider the vertices
          in order of decreasing f[u] (as computed in line 1)
4  output the vertices of each tree in the depth-first forest formed in line 3 as a
          separate strongly connected component

The idea behind this algorithm comes from a key property of the component graph G^SCC = (V^SCC, E^SCC), which we define as follows. Suppose that G has strongly connected components C₁, C₂,..., C_k. The vertex set V^SCC is {v₁, v₂,..., v_k}, and it contains a vertex v_i for each strongly connected component C_i of G. There is an edge (v_i, v_j) ∈ E^SCC if G contains a directed edge (x, y) for some x ∈ C_i and some y ∈ C_j. Looked at another way, by contracting all edges whose incident vertices are within the same strongly connected component of G, the resulting graph is G^SCC. Figure 22.9(c) shows the component graph of the graph in Figure 22.9(a).

The key property is that the component graph is a dag, which the following lemma implies. Articulation points, bridges, and biconnected components

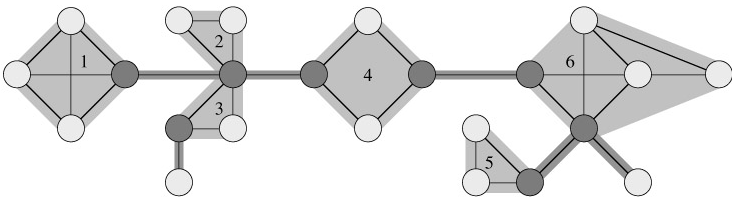
Let G = (V, E) be a connected, undirected graph. An articulation point of G is a vertex whose removal disconnects G. A bridge of G is an edge whose removal disconnects G. A biconnected component of G is a maximal set of edges such that any two edges in the set lie on a common simple cycle. Figure 22.10 illustrates these definitions. We can determine articulation points, bridges, and biconnected components using depth-first search. Let G_π = (V, E_π) be a depth-first tree of G.

Figure 22.10: The articulation points, bridges, and biconnected components of a connected, undirected graph for use in Problem 22-2. The articulation points are the heavily shaded vertices, the bridges are the heavily shaded edges, and the biconnected components are the edges in the shaded regions, with a bcc numbering shown.

Prove that the root of G_π is an articulation point of G if and only if it has at least two children in G_π.
Let v be a nonroot vertex of G_π. Prove that v is an articulation point of G if and only if v has a child s such that there is no back edge from s or any descendant of s to a proper ancestor of v.
Let
Show how to compute low[v] for all vertices v ∈ V in O(E) time.
Show how to compute all articulation points in O(E) time.
Prove that an edge of G is a bridge if and only if it does not lie on any simple cycle of G.
Show how to compute all the bridges of G in O(E) time.
Prove that the biconnected components of G partition the nonbridge edges of G.
Give an O(E)-time algorithm to label each edge e of G with a positive integer bcc[e] such that bcc[e] = bcc[e′] if and only if e and e′ are in the same biconnected component.