The Dft And Fft

By the halving lemma, the list of values (30.10) consists not of n distinct values but only of the n/2 complex (n/2)th roots of unity, with each root occurring exactly twice. Therefore, the polynomials A^[0] and A^[1] of degree-bound n/2 are recursively evaluated at the n/2 complex (n/2)th roots of unity. These subproblems have exactly the same form as the original problem, but are half the size. We have now successfully divided an n-element DFT_n computation into two n/2-element DFT_n/2 computations. This decomposition is the basis for the following recursive FFT algorithm, which computes the DFT of an n-element vector a = (a₀, a₁,..., a_n-1), where n is a power of 2.

	RECURSIVE-FFT(a)
 1  n ← length[a]     ▹ n is a power of 2.
 2  if n = 1
 3     then return a
 4  wn ← eπi/n
 5  w ← 1
 6  a[0] ← (a0, a2,..., an-2)
 7  a[1] ← (a1, a3,..., an-1)
 8  y[0] ← RECURSIVE-FFT(a[0])
 9  y[1] RECURSIVE-FFT(a[1])
10  for k ← 0 to n/2 - 1
11       do 

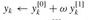
	12          

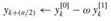
	13          w ← w wn
14  return y       ▹ y is assumed to be a column vector.

The RECURSIVE-FFT procedure works as follows. Lines 2 -3 represent the basis of the recursion; the DFT of one element is the element itself, since in this case

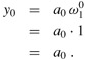
Lines 6 -7 define the coefficient vectors for the polynomials A^[0] and A^[1]. Lines 4, 5, and 13 guarantee that w is updated properly so that whenever lines 11 -12 are executed, . (Keeping a running value of w from iteration to iteration saves time over computing 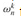from scratch each time through the for loop.) Lines 8-9 perform the recursive DFT_n/2 computations, setting, for k = 0, 1,..., n/2 - 1,

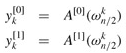
or, since 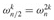by the cancellation lemma,

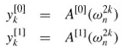
Lines 11-12 combine the results of the recursive DFT_n/2 calculations. For y₀, y₁,..., y_n/2-1, line 11 yields

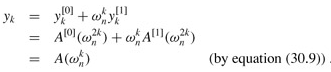
For y_n/2, y_{n/2 1},..., y_n-1, letting k = 0, 1,..., n/2 - 1, line 12 yields

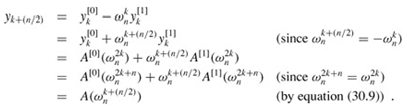
Thus, the vector y returned by RECURSIVE-FFT is indeed the DFT of the input vector a.