The Potential Method
The potential method: Instead of representing prepaid work as credit stored with specific objects in the data structure, the potential method of amortized analysis represents the prepaid work as "potential energy," or just "potential," that can be released to pay for future operations. The potential is associated with the data structure as a whole rather than with specific objects within the data structure.
The potential method works as follows. We start with an initial data structure D0 on which n operations are performed. For each i = 1, 2, ..., n, we let ci be the actual cost of the ith operation and Di be the data structure that results after applying the ith operation to data structure Di-1. A potential function Φ maps each data structure Di to a real number Φ(Di), which is the potential associated with data structure Di. The amortized cost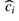 
of the ith operation with respect to potential function Φ is defined by
The amortized cost of each operation is therefore its actual cost plus the increase in potential due to the operation. By equation (17.2), the total amortized cost of the n operations is
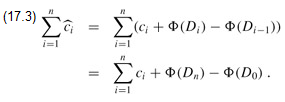
The second equality follows from equation (A.9), since the Φ(Di) terms telescope.
If we can define a potential function Φ so that Φ(Dn) ≥ Φ(D0), then the total amortized cost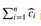 
is an upper bound on the total actual cost 
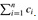. In practice, we do not always know how many operations might be performed. Therefore, if we require that Φ (Di) ≥ Φ (D0) for all i, then we guarantee, as in the accounting method, that we pay in advance. It is often convenient to define Φ (D0) to be 0 and then to show that Φ (Di) ≥ 0 for all i.
Intuitively, if the potential difference Φ(Di) - Φ(Di-1) of the ith operation is positive, then the amortized cost 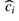represents an overcharge to the ith operation, and the potential of the data structure increases. If the potential difference is negative, then the amortized cost represents an undercharge to the ith operation, and the actual cost of the operation is paid by the decrease in the potential.
The amortized costs defined by equations (17.2) and (17.3) depend on the choice of the potential function Φ. Different potential functions may yield different amortized costs yet still be upper bounds on the actual costs. There are often trade-offs that can be made in choosing a potential function; the best potential function to use depends on the desired time bounds.
Stack operations: To illustrate the potential method, we return once again to the example of the stack operations PUSH, POP, and MULTIPOP. We define the potential function Φ on a stack to be the number of objects in the stack. For the empty stack D0 with which we start, we have Φ(D0) = 0. Since the number of objects in the stack is never negative, the stack Di that results after the ith operation has nonnegative potential, and thus
|
Φ(Di) |
≥ |
0 |
|
= |
Φ(D0). |
The total amortized cost of n operations with respect to Φ therefore represents an upper bound on the actual cost.
Let us now compute the amortized costs of the various stack operations. If the ith operation on a stack containing s objects is a PUSH operation, then the potential difference is
|
Φ(Di) - Φ(Di-1) |
= |
(s 1) -s |
|
= |
1 |
By equation (17.2), the amortized cost of this PUSH operation is
|
|
= |
ci Φ(Di) - Φ (Di-1) |
|
= |
1 1 |
|
|
= |
2 |