The Set-covering Problem
The set-covering problem: The set-covering problem is an optimization problem that models many resource-selection problems. Its corresponding decision problem generalizes the NP-complete vertex-cover problem and is therefore also NP-hard. The approximation algorithm developed to handle the vertex-cover problem doesn't apply here, however, and so we need to try other approaches. We shall examine a simple greedy heuristic with a logarithmic approximation ratio. That is, as the size of the instance gets larger, the size of the approximate solution may grow, relative to the size of an optimal solution. Because the logarithm function grows rather slowly, however, this approximation algorithm may nonetheless give useful results.
An instance (X, 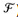 ) of the set-covering problem consists of a finite set X and a family
) of the set-covering problem consists of a finite set X and a family 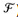 of subsets of X, such that every element of X belongs to at least one subset in
of subsets of X, such that every element of X belongs to at least one subset in 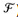 :
:
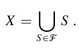
We say that a subset 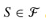 covers its elements. The problem is to find a minimum-size subset
covers its elements. The problem is to find a minimum-size subset 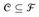 whose members cover all of X:
whose members cover all of X:
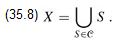
We say that any 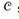 satisfying equation (35.8) covers X. Figure 35.3 illustrates the set-covering problem. The size of
satisfying equation (35.8) covers X. Figure 35.3 illustrates the set-covering problem. The size of 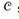 is defined as the number of sets it contains, rather than the number of individual elements in these sets. In Figure 35.3, the minimum set cover has size 3.
is defined as the number of sets it contains, rather than the number of individual elements in these sets. In Figure 35.3, the minimum set cover has size 3.
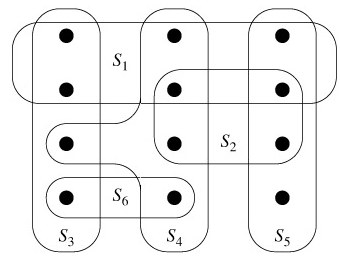
Figure 35.3: An instance (X,
 ) of the set-covering problem, where X consists of the 12 black points and
) of the set-covering problem, where X consists of the 12 black points and 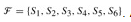 . A minimum-size set cover is
. A minimum-size set cover is 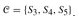 . The greedy algorithm produces a cover of size 4 by selecting the sets S1, S4, S5, and S3 in order.
. The greedy algorithm produces a cover of size 4 by selecting the sets S1, S4, S5, and S3 in order.The set-covering problem is an abstraction of many commonly arising combinatorial problems. As a simple example, suppose that X represents a set of skills that are needed to solve a problem and that we have a given set of people available to work on the problem. We wish to form a committee, containing as few people as possible, such that for every requisite skill in X, there is a member of the committee having that skill. In the decision version of the set-covering problem, we ask whether or not a covering exists with size at most k, where k is an additional parameter specified in the problem instance. The decision version of the problem is NP-complete.
A greedy approximation algorithm
The greedy method works by picking, at each stage, the set S that covers the greatest number of remaining elements that are uncovered.
GREEDY-SET-COVER(X,
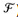
)
1 U ← X
2
3 while U ≠ Ø 4 do select an
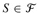
that maximizes |S ∪ U | 5 U ← U - S 6
7 return
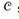
In the example of Figure 35.3, GREEDY-SET-COVER adds to 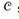 the sets S1, S4, S5, and S3, in order.
the sets S1, S4, S5, and S3, in order.
The algorithm works as follows. The set U contains, at each stage, the set of remaining uncovered elements. The set 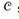 contains the cover being constructed. Line 4 is the greedy decision-making step. A subset S is chosen that covers as many uncovered elements as possible (with ties broken arbitrarily). After S is selected, its elements are removed from U , and S is placed in
contains the cover being constructed. Line 4 is the greedy decision-making step. A subset S is chosen that covers as many uncovered elements as possible (with ties broken arbitrarily). After S is selected, its elements are removed from U , and S is placed in 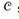 . When the algorithm terminates, the set
. When the algorithm terminates, the set 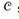 contains a subfamily of
contains a subfamily of 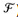 that covers X.
that covers X.
The algorithm GREEDY-SET-COVER can easily be implemented to run in time polynomial in |X| and |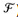 |. Since the number of iterations of the loop on lines 3-6 is bounded from above by min(|X| , |
|. Since the number of iterations of the loop on lines 3-6 is bounded from above by min(|X| , |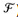 |), and the loop body can be implemented to run in time O(|X||
|), and the loop body can be implemented to run in time O(|X||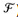 |), there is an implementation that runs in time O(|X||
|), there is an implementation that runs in time O(|X||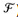 | min(|X|, |
| min(|X|, |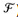 |)).
|)).
Analysis: We now show that the greedy algorithm returns a set cover that is not too much larger than an optimal set cover. For convenience, in this chapter we denote the dth harmonic number 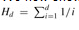 by H (d). As a boundary condition, we define H (0) = 0.
by H (d). As a boundary condition, we define H (0) = 0.