The Substitution Method For Recurrences

Subtleties: There are times when you can correctly guess at an asymptotic bound on the solution of a recurrence, but somehow the math doesn't seem to work out in the induction. Usually, the problem is that the inductive assumption isn't strong enough to prove the detailed bound. When you hit such a snag, revising the guess by subtracting a lower-order term often permits the math to go through.

Consider the recurrence

T (n) = T (⌊n/2⌋) T (⌈n/2⌉) 1.

We guess that the solution is O(n), and we try to show that T (n) ≤ cn for an appropriate choice of the constant c. Substituting our guess in the recurrence, we obtain

which does not imply T (n) ≤ cn for any choice of c. It's tempting to try a larger guess, say T (n) = O(n2), which can be made to work, but in fact, our guess that the solution is T (n) = O(n) is correct. In order to show this, however, we must make a stronger inductive hypothesis.

Intuitively, our guess is nearly right: we're only off by the constant 1, a lower-order term. Nevertheless, mathematical induction doesn't work unless we prove the exact form of the inductive hypothesis. We overcome our difficulty by subtracting a lower-order term from our previous guess. Our new guess is T (n) ≤ cn - b, where b ≥ 0 is constant. We now have

as long as b ≥ 1. As before, the constant c must be chosen large enough to handle the boundary conditions.

Most people find the idea of subtracting a lower-order term counterintuitive. After all, if the math doesn't work out, shouldn't we be increasing our guess? The key to understanding this step is to remember that we are using mathematical induction: we can prove something stronger for a given value by assuming something stronger for smaller values.

Avoiding pitfalls: It is easy to err in the use of asymptotic notation. For example, in the recurrence (4.4) we can falsely "prove" T (n) = O(n) by guessing T (n) ≤ cn and then arguing

since c is a constant. The error is that we haven't proved the exact form of the inductive hypothesis, that is, that T (n) ≤ cn.

Changing variables: Sometimes, a little algebraic manipulation can make an unknown recurrence similar to one you have seen before. As an example, consider the recurrence

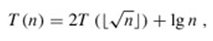
which looks difficult. We can simplify this recurrence, though, with a change of variables. For convenience, we shall not worry about rounding off values, such as , to be integers. Renaming m = lg n yields

T (2m) = 2T (2m/2) m.

We can now rename S(m) = T(2m) to produce the new recurrence

S(m) = 2S(m/2) m,

which is very much like recurrence (4.4). Indeed, this new recurrence has the same solution: S(m) = O(m lg m). Changing back from S(m) to T (n), we obtain T (n) = T (2m) = S(m) = O(m lg m) = O(lg n lg lg n).