The Vertex-cover Problem

The vertex-cover problem: The vertex-cover problem was defined and proven NP-complete in vertex-cover problem. A vertex cover of an undirected graph G = (V, E) is a subset V′ ⊆ V such that if (u, v) is an edge of G, then either u ∈ V′ or v ∈ V′ (or both). The size of a vertex cover is the number of vertices in it.

The vertex-cover problem is to find a vertex cover of minimum size in a given undirected graph. We call such a vertex cover an optimal vertex cover. This problem is the optimization version of an NP-complete decision problem.

Even though it may be difficult to find an optimal vertex cover in a graph G, it is not too hard to find a vertex cover that is near-optimal. The following approximation algorithm takes as input an undirected graph G and returns a vertex cover whose size is guaranteed to be no more than twice the size of an optimal vertex cover.

	APPROX-VERTEX-COVER(G">
1  C ← Ø
2  E′ ← E[G]
3  while E′ ≠ Ø
4     do let (u, v) be an arbitrary edge of E′
5        C ← C ∪ {u, v}
6        remove from E′ every edge incident on either u or v
7  return C

Figure 35.1 illustrates the operation of APPROX-VERTEX-COVER. The variable C contains the vertex cover being constructed. Line 1 initializes C to the empty set. Line 2 sets E′ to be a copy of the edge set E[G] of the graph. The loop on lines 3-6 repeatedly picks an edge (u, v) from E′, adds its endpoints u and v to C, and deletes all edges in E′ that are covered by either u or v. The running time of this algorithm is O(V E), using adjacency lists to represent E′.

Figure 35.1: The operation of APPROX-VERTEX-COVER. (a) The input graph G, which has 7 vertices and 8 edges. (b) The edge (b, c), shown heavy, is the first edge chosen by APPROX-VERTEX-COVER. Vertices b and c, shown lightly shaded, are added to the set C containing the vertex cover being created. Edges (a, b), (c, e), and (c, d), shown dashed, are removed since they are now covered by some vertex in C. (c) Edge (e, f) is chosen; vertices e and f are added to C. (d) Edge (d, g) is chosen; vertices d and g are added to C. (e) The set C, which is the vertex cover produced by APPROX-VERTEX-COVER, contains the six vertices b, c, d, e, f, g. (f) The optimal vertex cover for this problem contains only three vertices: b, d, and e.

The vertex-cover problem: A vertex cover of an undirected graph G = (V, E) is a subset V' ⊆ V such that if (u, v) ∈ E, then u ∈ V' or v ∈ V' (or both). That is, each vertex "covers" its incident edges, and a vertex cover for G is a set of vertices that covers all the edges in E. The size of a vertex cover is the number of vertices in it. For example, the graph in Figure 34.15(b) has a vertex cover {w, z} of size 2.

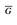Figure 34.15: Reducing CLIQUE to VERTEX-COVER. (a) An undirected graph G = (V, E) with clique V' = {u, v, x, y}. (b) The graph produced by the reduction algorithm that has vertex cover V - V' = {w, z}.

The vertex-cover problem is to find a vertex cover of minimum size in a given graph. Restating this optimization problem as a decision problem, we wish to determine whether a graph has a vertex cover of a given size k. As a language, we define

VERTEX-COVER = {〈G, k〉 : graph G has a vertex cover of size k}.