A Shortest-path Algorithm (Dijkstra’s Algorithm.)
Introduction: Dijkstra’s Algorithm is describe solves this problem in undirected weighted graphs where all the weights are positive. It is easy to adapt it to solve shortest-path problems in directed graphs.
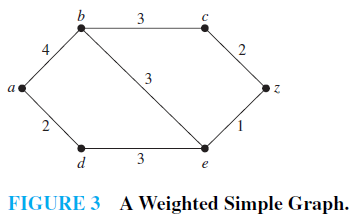
EXAMPLE 1 What is the length of a shortest path between a and z in the weighted graph shown in Figure 3?
Solution: Although a shortest path is easily found by inspection, we will develop some ideas useful in understanding Dijkstra’s algorithm. We will solve this problem by finding the length of a shortest path from a to successive vertices, until z is reached. The only paths starting at a that contain no vertex other than a are formed by adding an edge that has a as one endpoint. These paths have only one edge. They are a, b of length 4 and a, d of length 2. It follows that d is the closest vertex to a, and the shortest path from a to d has length 2.
We can find the second closest vertex by examining all paths that begin with the shortest path from a to a vertex in the set {a, d}, followed by an edge that has one endpoint in {a, d} and its other endpoint not in this set. There are two such paths to consider, a, d, e of length 7 and a, b of length 4. Hence, the second closest vertex to a is b and the shortest path from a to b has length 4.
To find the third closest vertex to a, we need examine only the paths that begin with the shortest path from a to a vertex in the set {a, d, b}, followed by an edge that has one endpoint in the set {a, d, b} and its other endpoint not in this set. There are three such paths, a, b, c of length 7, a, b, e of length 7, and a, d, e of length 5. Because the shortest of these paths is a, d, e, the third closest vertex to a is e and the length of the shortest path from a to e is 5.
To find the fourth closest vertex to a, we need examine only the paths that begin with the shortest path from a to a vertex in the set {a, d, b, e}, followed by an edge that has one endpoint in the set {a, d, b, e} and its other endpoint not in this set. There are two such paths, a, b, c of length 7 and a, d, e, z of length 6. Because the shorter of these paths is a, d, e, z, the fourth closest vertex to a is z and the length of the shortest path from a to z is 6.
ALGORITHM 1 Dijkstra’s Algorithm.
- procedure Dijkstra(G: weighted connected simple graph, with all weights positive)
- {G has vertices a = v0, v1, . . . , vn = z and lengths w(vi , vj )
- where w(vi , vj )=∞if {vi , vj } is not an edge in G}
- for i := 1 to n
- L(vi ) :=∞
- L(a) := 0
- S := ∅
- {the labels are now initialized so that the label of a is 0 and all other labels are∞, and S is the empty set}
- while z
- ∈ S
- u := a vertex not in S with L(u) minimal
- S := S ∪ {u}
- for all vertices v not in S
- if L(u) w(u, v) < L(v) then L(v) := L(u) w(u, v)
- {this adds a vertex to S with minimal label and updates the labels of vertices not in S}
- return L(z) {L(z) = length of a shortest path from a to z}
Example 2 illustrates how Dijkstra’s algorithm works. Afterward, we will show that this algorithm always produces the length of a shortest path between two vertices in a weighted graph.
EXAMPLE 2 Use Dijkstra’s algorithm to find the length of a shortest path between the vertices a and z in the weighted graph displayed in Figure 4(a).
Solution: The steps used by Dijkstra’s algorithm to find a shortest path between a and z are shown in Figure 4. At each iteration of the algorithm the vertices of the set Sk are circled. A shortest path from a to each vertex containing only vertices in Sk is indicated for each iteration. The algorithm terminates when z is circled.We find that a shortest path from a to z is a, c, b, d, e, z, with length 13.
Remark: In performing Dijkstra’s algorithm it is sometimes more convenient to keep track of labels of vertices in each step using a table instead of redrawing the graph for each step.
Next, we use an inductive argument to show that Dijkstra’s algorithm produces the length of a shortest path between two vertices a and z in an undirected connected weighted graph. Take as the inductive hypothesis the following assertion: At the kth iteration
(i ) the label of every vertex v in S is the length of a shortest path from a to this vertex, and
(ii ) the label of every vertex not in S is the length of a shortest path from a to this vertex that contains only (besides the vertex itself) vertices in S.
When k = 0, before any iterations are carried out, S = ∅, so the length of a shortest path from a to a vertex other than a is∞. Hence, the basis case is true.