Bipartite Graphs And Matchings

Bipartite Graphs and Matchings: Bipartite graphs can be used to model many types of applications that involve matching the elements of one set to elements of another, as Example 14 illustrates.

EXAMPLE 1. Job Assignments Suppose that there are m employees in a group and n different jobs that need to be done, where m ≥ n. Each employee is trained to do one or more of these n jobs.We would like to assign an employee to each job. To help with this task, we can use a graph to model employee capabilities. We represent each employee by a vertex and each job by a vertex. For each employee, we include an edge from that employee to all jobs that the employee has been
trained to do. Note that the vertex set of this graph can be partitioned into two disjoint sets, the set of employees and the set of jobs, and each edge connects an employee to a job. Consequently, this graph is bipartite, where the bipartition is (E, J ) where E is the set of employees and J is the set of jobs.We now consider two different scenarios.

First, suppose that a group has four employees: Alvarez, Berkowitz, Chen, and Davis; and suppose that four jobs need to be done to complete Project 1: requirements, architecture, implementation, and testing. Suppose that Alvarez has been trained to do requirements and testing; Berkowitz has been trained to do architecture, implementation, and testing; Chen has been trained to do requirements, architecture, and implementation; and Davis has only been trained to do requirements. We model these employee capabilities using the bipartite graph in Figure 10(a).

Second, suppose that a group has second group also has four employees:Washington, Xuan, Ybarra, and Ziegler; and suppose that the same four jobs need to be done to complete Project 2 as are needed to complete Project 1. Suppose thatWashington has been trained to do architecture; Xuan has been trained to do requirements, implementation, and testing; Ybarra has been trained to do architecture; and Ziegler has been trained to do requirements, architecture and testing.We model these employee capabilities using the bipartite graph in Figure 10(b). To complete Project 1, we must assign an employee to each job so that every job has an employee assigned to it, and so that no employee is assigned more than one job.We can do this by assigning Alvarez to testing, Berkowitz to implementation, Chen to architecture, and Davis to requirements, as shown in Figure 10(a) (where blue lines show this assignment of jobs). To complete Project 2, we must also assign an employee to each job so that every job has an employee assigned to it and no employee is assigned more than one job. However, this is

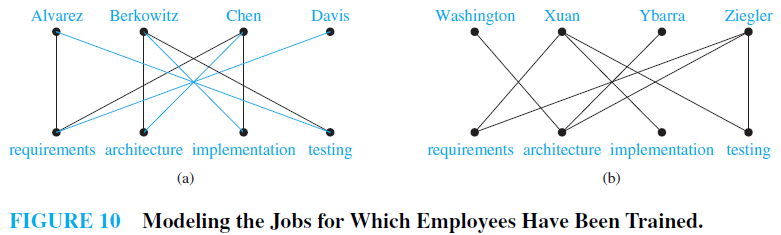
impossible because there are only two employees, Xuan and Ziegler, who have been trained for at least one of the three jobs of requirements, implementation, and testing. Consequently, there is no way to assign three different employees to these three job so that each job is assigned an employee with the appropriate training.

Finding an assignment of jobs to employees can be thought of as finding a matching in the graph model, where a matching M in a simple graph G = (V ,E) is a subset of the set E of edges of the graph such that no two edges are incident with the same vertex. In other words, a matching is a subset of edges such that if {s, t} and {u, v} are distinct edges of the matching, then s, t , u, and v are distinct.A vertex that is the endpoint of an edge of a matchingM is said to be matched in M; otherwise it is said to be unmatched. A maximum matching is a matching with the largest number of edges. We say that a matching M in a bipartite graph G = (V ,E) with bipartition (V1, V2) is a complete matching from V1 to V2 if every vertex in V1 is the endpoint of an edge in the matching, or equivalently, if |M| = |V1|. For example, to assign jobs to employees so that the largest number of jobs are assigned employees, we seek a maximum matching in the graph that models employee capabilities. To assign employees to all jobs we seek a complete matching from the set of jobs to the set of employees. In Example 14, we found a complete matching from the set of jobs to the set of employees for Project 1, and this matching is a maximun matching, and we showed that no complete matching exists from the set of jobs to the employees for Project 2.

We now give an example of how matchings can be used to model marriages.

NECESSARY AND SUFFICIENT CONDITIONS FOR COMPLETE MATCHINGS We now turn our attention to the question of determining whether a complete matching from V1 to V2 exists when (V1, V2) is a bipartition of a bipartite graph G = (V ,E).We will introduce a theorem that provides a set of necessary and sufficient conditions for the existence of a complete matching. This theorem was proved by Philip Hall in 1935.