Cartesian Product Of Lattices

Cartesian Product of Lattices
Theorem: If (L1, ≤) and (L2, ≤) are lattices, then (L, ≤) is a lattice, where L = L1 X L2 and the partial order ≤ of L is the product partial order.

Proof: We denote the join and meet in L1 by ∨1, and ∧1 and the join and meet in L2 by ∨2 and ∧2 respectively. We know that Cartesian product of two posets is a poset. Therefore L = L1 X L2 is a poset. Thus all we need to show is that if (a1, b1) and (a2, b2) Î L, then (a1, b1) Ú (a2, b2)and (a1, b1) ∈ (a2, b2) exist in L.

Further, we know that

(a1, b1) ∨ (a2, b2) = (a1 ∨ 1 a2 , b1 ∨ 2 b2)
and
(a1, b1) ∧ (a2, b2) = (a1 ∧ 1 a2 , b1 ∧ 2 b2)

Since L1 is lattice, a1 ∨ 1 a2 and a1 ∧ 1 a2 exist. Similarly, since L2 is a lattice, b1 ∨ 2 b2 and b1 ∧ 2 b2 exist. Hence (a1, b1) ∨ (a2, b2) and (a1, b1) ∧ (a2, b2) both exist and therefore (L, ≤) is a lattice, called the direct product of (L1, ≤) and (L2, ≤).

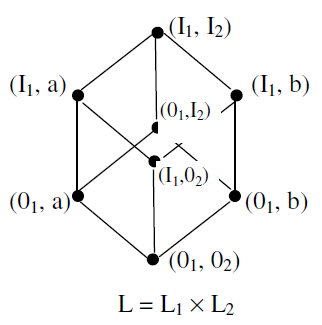
Example: Let L1 and L2 be the lattices whose Hasse diagram are given below :

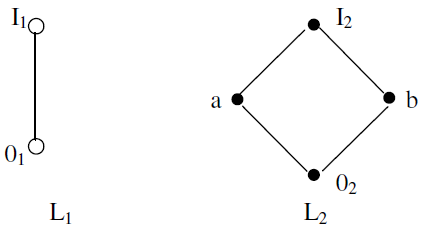
Then L = L1 X L2 is the lattice shown in the diagram below: