Conditional Statements

DEFINITION 1 Let p and q be propositions. The conditional statement p → q is the proposition “if p, then q.” The conditional statement p → q is false when p is true and q is false, and true otherwise. In the conditional statement p → q, p is called the hypothesis (or antecedent or premise) and q is called the conclusion (or consequence).

The statement p → q is called a conditional statement because p → q asserts that q is true on the condition that p holds. A conditional statement is also called an implication. The truth table for the conditional statement p → q is shown in Table 5. Note that the statement p → q is true when both p and q are true and when p is false (no matter what truth value q has).

Because conditional statements play such an essential role in mathematical reasoning, a variety of terminology is used to express p → q. You will encounter most if not all of the following ways to express this conditional statement:

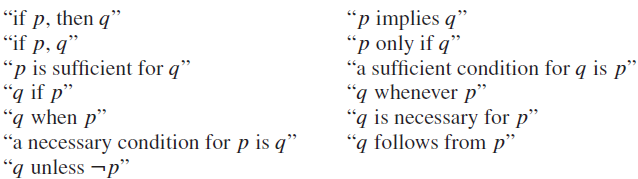
A useful way to understand the truth value of a conditional statement is to think of an obligation or a contract. For example, the pledge many politicians make when running for office is “If I am elected, then I will lower taxes.”

If the politician is elected, voters would expect this politician to lower taxes. Furthermore, if the politician is not elected, then voters will not have any expectation that this person will lower taxes, although the person may have sufficient influence to cause those in power to lower taxes. It is only when the politician is elected but does not lower taxes that voters can say that the politician has broken the campaign pledge. This last scenario corresponds to the case when p is true but q is false in p → q.
Similarly, consider a statement that a professor might make:
“If you get 100% on the final, then you will get an A.”
If you manage to get a 100% on the final, then you would expect to receive an A. If you do not get 100% you may or may not receive an A depending on other factors. However, if you do get 100%, but the professor does not give you an A, you will feel cheated. Of the various ways to express the conditional statement p → q, the two that seem to cause the most confusion are “p only if q” and “q unless ¬p.” Consequently, we will provide some guidance for clearing up this confusion.

To remember that “p only if q” expresses the same thing as “if p, then q,” note that “p only if q” says that p cannot be true when q is not true. That is, the statement is false if p is true, but q is false. When p is false, q may be either true or false, because the statement says nothing about the truth value of q. Be careful not to use “q only if p” to express p → q because this is incorrect. To see this, note that the true values of “q only if p” and p → q are different when p and q have different truth values.

To remember that “q unless ¬p” expresses the same conditional statement as “if p, then q,” note that “q unless ¬p” means that if ¬p is false, then q must be true. That is, the statement “q unless ¬p” is false when p is true but q is false, but it is true otherwise. Consequently, “q unless ¬p” and p → q always have the same truth value. We illustrate the translation between conditional statements and English statements in Example 1.

EXAMPLE 1 Let p be the statement “Maria learns discrete mathematics” and q the statement “Maria will find a good job.” Express the statement p → q as a statement in English.
Solution: From the definition of conditional statements, we see that when p is the statement “Maria learns discrete mathematics” and q is the statement “Maria will find a good job,” p → q represents the statement
“If Maria learns discrete mathematics, then she will find a good job.”
There are many other ways to express this conditional statement in English. Among the most natural of these are:
“Maria will find a good job when she learns discrete mathematics.”
“For Maria to get a good job, it is sufficient for her to learn discrete mathematics.” and
“Maria will find a good job unless she does not learn discrete mathematics.”

Note that the way we have defined conditional statements is more general than the meaning attached to such statements in the English language. For instance, the conditional statement in Example 1 and the statement “If it is sunny, then we will go to the beach.” are statements used in normal language where there is a relationship between the hypothesis and the conclusion. Further, the first of these statements is true unless Maria learns discrete mathematics, but she does not get a good job, and the second is true unless it is indeed sunny, but we do not go to the beach. On the other hand, the statement

“If Juan has a smartphone, then 2 3 = 5” is true from the definition of a conditional statement, because its conclusion is true. (The truth value of the hypothesis does not matter then.) The conditional statement “If Juan has a smartphone, then 2 3 = 6” is true if Juan does not have a smartphone, even though 2 3 = 6 is false. We would not use these last two conditional statements in natural language (except perhaps in sarcasm), because there is no relationship between the hypothesis and the conclusion in either statement. In mathematical reasoning, we consider conditional statements of a more general sort than we use in English. The mathematical concept of a conditional statement is independent of a cause-andeffect relationship between hypothesis and conclusion. Our definition of a conditional statement specifies its truth values; it is not based on English usage. Propositional language is an artificial language; we only parallel English usage to make it easy to use and remember.

CONVERSE, CONTRAPOSITIVE, AND INVERSE We can form some new conditional statements starting with a conditional statement p → q. In particular, there are three related conditional statements that occur so often that they have special names. The proposition q → p is called the converse of p → q. The contrapositive of p → q is the proposition ¬q →¬p. The proposition ¬p →¬q is called the inverse of p → q. We will see that of these three conditional statements formed from p → q, only the contrapositive always has the same truth value as p → q. We first show that the contrapositive, ¬q →¬p, of a conditional statement p → q always has the same truth value as p → q. To see this, note that the contrapositive is false only when ¬p is false and ¬q is true, that is, only when p is true and q is false.We now show that neither the converse, q → p, nor the inverse, ¬p →¬q, has the same truth value as p → q for all possible truth values of p and q. Note that when p is true and q is false, the original conditional statement is false, but the converse and the inverse are both true.

When two compound propositions always have the same truth value we call them equivalent, so that a conditional statement and its contrapositive are equivalent. The converse and the inverse of a conditional statement are also equivalent, as the reader can verify, but neither is equivalent to the original conditional statement. (We will study equivalent propositions in Section 1.3.) Take note that one of the most common logical errors is to assume that the converse or the inverse of a conditional statement is equivalent to this conditional statement. We illustrate the use of conditional statements in Example 9.