Connectedness In Undirected Graphs

Connectedness in Undirected Graphs: When does a computer network have the property that every pair of computers can share information, if messages can be sent through one or more intermediate computers? When a graph is used to represent this computer network, where vertices represent the computers and edges represent the communication links, this question becomes: When is there always a path between two vertices in the graph?

DEFINITION 1 An undirected graph is called connected if there is a path between every pair of distinct vertices of the graph. An undirected graph that is not connected is called disconnected. We say that we disconnect a graph when we remove vertices or edges, or both, to produce a disconnected subgraph.
Thus, any two computers in the network can communicate if and only if the graph of this network is connected.

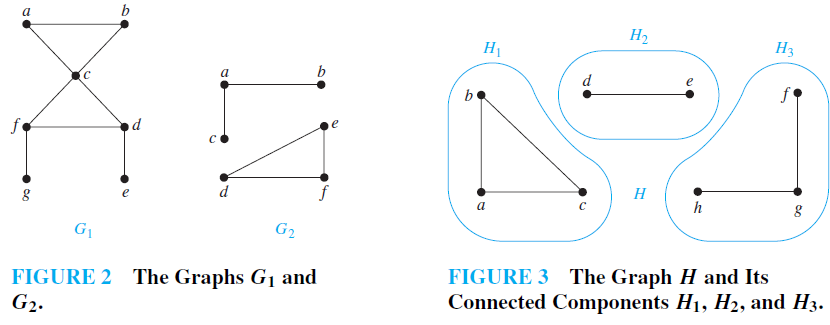
EXAMPLE 1 The graph G1 in Figure 2 is connected, because for every pair of distinct vertices there is a path between them (the reader should verify this). However, the graph G2 in Figure 2 is not connected. For instance, there is no path in G2 between vertices a and d.

THEOREM 1 There is a simple path between every pair of distinct vertices of a connected undirected graph.
Proof: Let u and v be two distinct vertices of the connected undirected graph G = (V ,E). BecauseGis connected, there is at least one path between u and v. Let x0, x1, . . . , xn, where x0 = u and xn = v, be the vertex sequence of a path of least length. This path of least length is simple. To see this, suppose it is not simple. Then xi = xj for some i and j with 0 ≤ i < j. This means that there is a path from u to v of shorter length with vertex sequence x0, x1, . . . , xi−1, xj , . . . , xn obtained by deleting the edges corresponding to the vertex sequence xi, . . . , xj−1.

CONNECTED COMPONENTS A connected component of a graph G is a connected subgraph of G that is not a proper subgraph of another connected subgraph of G. That is, a connected component of a graphGis a maximal connected subgraph ofG.A graphGthat is not connected has two or more connected components that are disjoint and have G as their union.

EXAMPLE 2 What are the connected components of the graph H shown in Figure 3?
Solution: The graphH is the union of three disjoint connected subgraphsH1,H2, andH3, shown in Figure 3. These three subgraphs are the connected components of H.

EXAMPLE 3 Connected Components of Call Graphs Two vertices x and y are in the same component of a telephone call graph (see Example 4 in Section 10.1) when there is a sequence of telephone calls beginning at x and ending at y. When a call graph for telephone calls made during a particular day in the AT&T network was analyzed, this graph was found to have 53,767,087 vertices, more than 170 million edges, and more than 3.7 million connected components. Most of these components were small; approximately three-fourths consisted of two vertices representing pairs of telephone numbers that called only each other. This graph has one huge connected component with 44,989,297 vertices comprising more than 80% of the total. Furthermore, every vertex in this component can be linked to any other vertex by a chain of no more than 20 calls.