Connectivity Of Graphs
Introduction: Sometimes the removal from a graph of a vertex and all incident edges produces a subgraph with more connected components. Such vertices are called cut vertices (or articulation points). The removal of a cut vertex from a connected graph produces a subgraph that is not connected. Analogously, an edge whose removal produces a graph with more connected components than in the original graph is called a cut edge or bridge. Note that in a graph representing a computer network, a cut vertex and a cut edge represent an essential router and an essential link that cannot fail for all computers to be able to communicate.
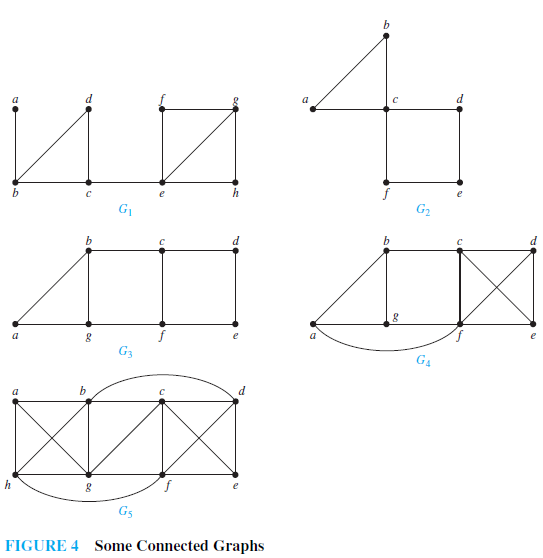
EXAMPLE 1 Find the cut vertices and cut edges in the graph G1 shown in Figure 4.
Solution: The cut vertices of G1 are b, c, and e. The removal of one of these vertices (and its adjacent edges) disconnects the graph. The cut edges are {a, b} and {c, e}. Removing either one of these edges disconnects G1.
VERTEX CONNECTIVITY Not all graphs have cut vertices. For example, the complete graph Kn, where n ≥ 3, has no cut vertices. When you remove a vertex from Kn and all edges incident to it, the resulting subgraph is the complete graph Kn−1, a connected graph. Connected graphs without cut vertices are called nonseparable graphs, and can be thought of as more connected than those with a cut vertex.We can extend this notion by defining a more granulated measure of graph connectivity based on the minimum number of vertices that can be removed to disconnect a graph.
A subset V' of the vertex set V of G = (V ,E) is a vertex cut, or separating set, if G − V' is disconnected. For instance, in the graph in Figure 1, the set {b, c, e} is a vertex cut with three vertices, as the reader should verify. We leave it to the reader (Exercise 51) to show that every connected graph, except a complete graph, has a vertex cut.We define the vertex connectivity of a noncomplete graph G, denoted by κ(G), as the minimum number of vertices in a vertex cut.
WhenGis a complete graph, it has no vertex cuts, because removing any subset of its vertices and all incident edges still leaves a complete graph. Consequently, we cannot define κ(G) as the minimum number of vertices in a vertex cut whenGis complete. Instead, we set κ(Kn) = n − 1, the number of vertices needed to be removed to produce a graph with a single vertex. Consequently, for every graph G, κ(G) is minimum number of vertices that can be removed from G to either disconnect G or produce a graph with a single vertex. We have 0 ≤ κ(G) ≤ n − 1 if G has n vertices, κ(G) = 0 if and only if G is disconnected or G = K1, and κ(G) = n − 1 if and only if G is complete.
The larger κ(G) is, the more connected we consider G to be. Disconnected graphs and K1 have κ(G) = 0, connected graphs with cut vertices and K2 have κ(G) = 1, graphs without cut vertices that can be disconnected by removing two vertices and K3 have κ(G) = 2, and so on.We say that a graph is k-connected (or k-vertex-connected), if κ(G) ≥ k. A graph G is 1- connected if it is connected and not a graph containing a single vertex; a graph is 2-connected, or biconnected, if it is nonseparable and has at least three vertices. Note that if G is a k-connected graph, then G is a j -connected graph for all j with 0 ≤ j ≤ k.
EXAMPLE 2 Find the vertex connectivity for each of the graphs in Figure 4.
Solution: Each of the five graphs in Figure 4 is connected and has more than vertex, so each of these graphs has positive vertex connectivity. Because G1 is a connected graph with a cut vertex, as shown in Example 7, we know that κ(G1) = 1. Similarly, κ(G2) = 1, because c is a cut vertex of G2.
The reader should verify that G3 has no cut vertices. but that {b, g} is a vertex cut. Hence, κ(G3) = 2. Similarly, because G4 has a vertex cut of size two, {c, f }, but no cut vertices. It follows that κ(G4) = 2. The reader can verify thatG5 has no vertex cut of size two, but {b, c, f } is a vertex cut of G5. Hence, κ(G5) = 3. ▲
EDGE CONNECTIVITY We can also measure the connectivity of a connected graph G = (V ,E) in terms of the minimum number of edges that we can remove to disconnect it. If a graph has a cut edge, then we need only remove it to disconnect G. If G does not have a cut edge, we look for the smallest set of edges that can be removed to disconnect it. A set of edges E' is called an edge cut of G if the subgraph G − E' is disconnected. The edge connectivity of a graph G, denoted by λ(G), is the minimum number of edges in an edge cut of G. This defines λ(G) for all connected graphs with more than one vertex because it is always possible to disconnect such a graph by removing all edges incident to one of its vertices. Note that λ(G) = 0 if G is not connected.We also specify that λ(G) = 0 if G is a graph consisting of a single vertex. It follows that if G is a graph with n vertices, then 0 ≤ λ(G) ≤ n − 1.We leave it to the reader [Exercise 52(b)] to show that λ(G) = n − 1 where G is a graph with n vertices if and only if G = Kn, which is equivalent to the statement that λ(G) ≤ n − 2 when G is not a complete graph.
EXAMPLE 3 Find the edge connectivity of each of the graphs in Figure 4.
Solution: Each of the five graphs in Figure 4 is connected and has more than one vertex, so we know that all of them have positive edge connectivity. As we saw in Example 1, G1 has a cut edge, so λ(G1) = 1. The graph G2 has no cut edges, as the reader should verify, but the removal of the two edges {a, b} and {a, c} disconnects it. Hence, λ(G2) = 2. Similarly, λ(G3) = 2, because G3 has no cut edges, but the removal of the two edges {b, c} and {f, g} disconnects it. The reader should verify that the removal of no two edges disconnects G4, but the removal of the three edges {b, c}, {a, f }, and {f, g} disconnects it. Hence, λ(G4) = 3. Finally, the reader should verify that λ(G5) = 3, because the removal of any two of its edges does not disconnect it, but the removal of {a, b}, {a, g}, and {a, h} does.