Directed Graph

Introduction: A directed graph (or digraph) (V ,E) consists of a nonempty set of vertices V and a set of directed edges (or arcs) E. Each directed edge is associated with an ordered pair of vertices. The directed edge associated with the ordered pair (u, v) is said to start at u and end at v.

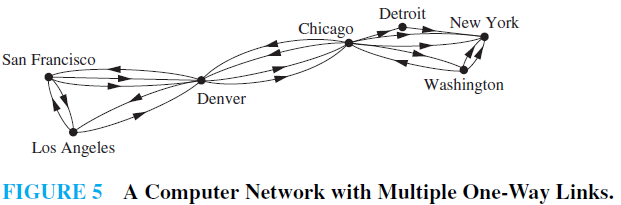
When we depict a directed graph with a line drawing, we use an arrow pointing from u to v to indicate the direction of an edge that starts at u and ends at v.A directed graph may contain loops and it may contain multiple directed edges that start and end at the same vertices.Adirected graph may also contain directed edges that connect vertices u and v in both directions; that is, when a digraph contains an edge from u to v, it may also contain one or more edges from v to u. Note that we obtain a directed graph when we assign a direction to each edge in an undirected graph.When a directed graph has no loops and has no multiple directed edges, it is called a simple directed graph. Because a simple directed graph has at most one edge associated to each ordered pair of vertices (u, v), we call (u, v) an edge if there is an edge associated to it in the graph. In some computer networks, multiple communication links between two data centers may be present, as illustrated in Figure 5. Directed graphs that may have multiple directed edges from a vertex to a second (possibly the same) vertex are used to model such networks.We called such graphs directed multigraphs. When there are m directed edges, each associated to an ordered pair of vertices (u, v), we say that (u, v) is an edge of multiplicity m.

For some models we may need a graph where some edges are undirected, while others are directed.Agraph with both directed and undirected edges is called a mixed graph. For example, a mixed graph might be used to model a computer network containing links that operate in both directions and other links that operate only in one direction.

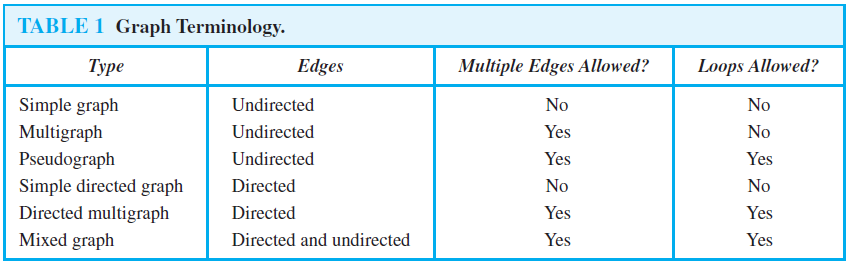
This terminology for the various types of graphs is summarized in Table 1.We will sometimes use the term graph as a general term to describe graphs with directed or undirected edges (or both), with or without loops, and with or without multiple edges. At other times, when the context is clear, we will use the term graph to refer only to undirected graphs.

Because of the relatively modern interest in graph theory, and because it has applications to a wide variety of disciplines, many different terminologies of graph theory have been introduced. The reader should determine how such terms are being used whenever they are encountered. The terminology used by mathematicians to describe graphs has been increasingly standardized, but the terminology used to discuss graphs when they are used in other disciplines is still quite varied. Although the terminology used to describe graphs may vary, three key questions can help us understand the structure of a graph: