Graph Models
BIOLOGICAL NETWORKS Many aspects of the biological sciences can be modeled using graphs.
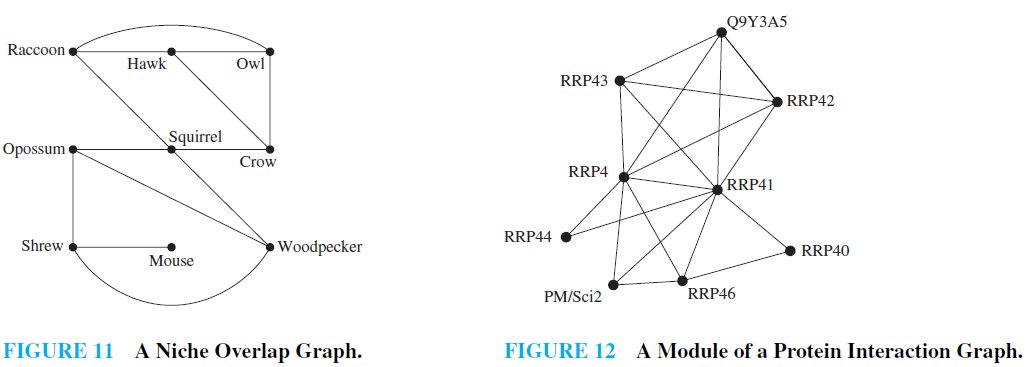
EXAMPLE 11 Niche Overlap Graphs in Ecology Graphs are used in many models involving the interaction of different species of animals. For instance, the competition between species in an ecosystem can be modeled using a niche overlap graph. Each species is represented by a vertex. An undirected edge connects two vertices if the two species represented by these vertices compete (that is, some of the food resources they use are the same). A niche overlap graph is a simple graph because no loops or multiple edges are needed in this model. The graph in Figure 11 models the ecosystem of a forest. We see from this graph that squirrels and raccoons compete but that crows and shrews do not.
EXAMPLE 12 Protein Interaction Graphs A protein interaction in a living cell occurs when two or more proteins in that cell bind to perform a biological function. Because protein interactions are crucial for most biological functions, many scientists work on discovering new proteins and understanding interactions between proteins. Protein interactions within a cell can be modeled using a protein interaction graph (also called a protein–protein interaction network), an undirected graph in which each protein is represented by a vertex, with an edge connecting the vertices representing each pair of proteins that interact. It is a challenging problem to determine genuine protein interactions in a cell, as experiments often produce false positives, which conclude that two proteins interact when they really do not. Protein interaction graphs can be used to deduce important biological information, such as by identifying the most important proteins for various functions and the functionality of newly discovered proteins.
Because there are thousands of different proteins in a typical cell, the protein interaction graph of a cell is extremely large and complex. For example, yeast cells have more than 6,000 proteins, and more than 80,000 interactions between them are known, and human cells have more than 100,000 proteins, with perhaps as many as 1,000,000 interactions between them. Additional vertices and edges are added to a protein interaction graph when new proteins and interactions between proteins are discovered. Because of the complexity of protein interaction graphs, they are often split into smaller graphs called modules that represent groups of proteins that are involved in a particular function of a cell. Figure 12 illustrates a module of the protein interaction graph described in [Bo04], comprising the complex of proteins that degrade RNA in human cells. To learn more about protein interaction graphs.
TOURNAMENTS We now give some examples that show how graphs can also be used to model different kinds of tournaments.
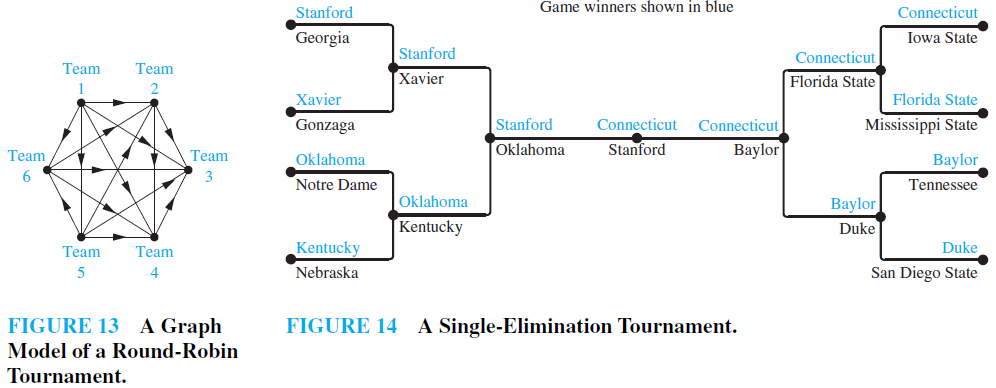
EXAMPLE 13 Round-Robin Tournaments A tournament where each team plays every other team exactly once and no ties are allowed is called a round-robin tournament. Such tournaments can be modeled using directed graphs where each team is represented by a vertex. Note that (a, b) is an edge if team a beats team b. This graph is a simple directed graph, containing no loops or multiple directed edges (because no two teams play each other more than once). Such a directed graph model is presented in Figure 13. We see that Team 1 is undefeated in this tournament, and Team 3 is winless.
EXAMPLE 14 Single-EliminationTournaments Atournament where each contestant is eliminated after one loss is called a single-elimination tournament. Single-elimination tournaments are often used in sports, including tennis championships and the yearly NCAA basketball championship. We can model such a tournament using a vertex to represent each game and a directed edge to connect a game to the next game the winner of this game played in. The graph in Figure 14 represents the games played by the final 16 teams in the 2010 NCAA women’s basketball tournament.