Homomorphisms And Normal Subgroups
Homomorphisms and normal subgroups: This section is similar to the corresponding one for rings. Homomorphisms are maps preserving the structure, while normal subgroups do the same job for groups as ideals do for rings: that is, they are kernels of homomorphisms.
Isomorphism: Just as for rings, we say that groups are isomorphic if there is a bijection between them which preserves the algebraic structure.
Formally, let G1 and G2 be groups. The map θ : G1 -> G2 is an isomorphism if it is a bijection from G1 to G2 and satisfies
(gh)θ = (gθ)(hθ) for all g,h∈G1.
Note that, as before, we write the map q to the right of its argument: that is, gq is the image of g under the map q. If there is an isomorphism from G1 to G2, we
say that the groups G1 and G1 are isomorphic.
Example Let G1 be the additive group of Z/2Z, and let G2 be the symmetric group S2. Their Cayley tables are:
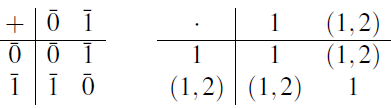
The map q that takes ¯0 to 1, and ¯1 to (1,2), is clearly an isomorphism from G1 to G2.
Homomorphisms
An isomorphism between groups has two properties: it is a bijection; and it preserves the group operation. If we relax the first property but keep the second, we obtain a homomorphism. Just as for rings, we say that a function q : G1 !G2 is
• a homomorphism if it satisfies (gh)θ = (gθ)(hθ);........... (3.1)
• a monomorphism if it satisfies (3.1) and is one-to-one;
• an epimorphism if it satisfies (3.1) and is onto;
• an isomorphism if it satisfies (3.1) and is one-to-one and onto.
We have the following lemma, proved in much the same way as for rings:
Lemma 3.17 Let q : G1 -> G2 be a homomorphism. Then 1θ = 1; (g−1)θ = (gθ)−1; and (gh−1)θ = (gθ)(hθ)−1, for all g,h ∈ G1. Now, if θ : G1 -> G2 is a homomorphism, we define the image of q to be the subset
{x ∈G2 : x = gθ for some g ∈ G1}
of G2, and the kernel of θ to be the subset
{g ∈ G1 : gθ = 1}
of G1.
Proposition 3.18 Let q : G1 -> G2 be a homomorphism.
(a) Im(θ) is a subgroup of G2.
(b) Ker(θ) is a subgroup of G1.
Proof We use the Second Subgroup Test in each case.
(a) Take x,y ∈ Im(θ), say x = gθ and y = hθ for g,h ∈ G1. Then xy−1 = (gh−1)θ ∈ Im(θ), by the Lemma.
(b) Take g,h ∈ Ker(θ). Then gθ =hθ =1, so (gh−1)θ =1−11=1; so gh−1 ∈ Ker(θ).
Example Look back to the Cayley table of the symmetric group S3 in Chapter 7. Colour the elements 1, (1,2,3) and (1,3,2) red, and the elements (1,2), (2,3) and (1,3) blue. We see that the Cayley table has the “simplified form”

This is a group of order ∈, and the map q taking 1, (1,2,3) and (1,3,2) to red and (1,2), (2,3) and (1,3) to blue is a homomorphism. Its kernel is the subgroup {1, (1,2,3), (1,3,2)}.