Incidence Matrices

Incidence Matrices: Another common way to represent graphs is to use incidence matrices. Let G = (V ,E) be an undirected graph. Suppose that v1, v2, . . . , vn are the vertices and e1, e2, . . . , em are the edges of G. Then the incidence matrix with respect to this ordering of V and E is the n × m matrix M = [mij ], where

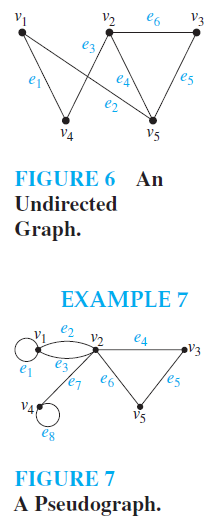
EXAMPLE 1 Represent the graph shown in Figure 6 with an incidence matrix.

Solution: The incidence matrix is

Incidence matrices can also be used to represent multiple edges and loops. Multiple edges are represented in the incidence matrix using columns with identical entries, because these edges are incident with the same pair of vertices. Loops are represented using a column with exactly one entry equal to 1, corresponding to the vertex that is incident with this loop.

EXAMPLE 2 Represent the pseudograph shown in Figure 7 using an incidence matrix.
Solution: The incidence matrix for this graph is