Introductio To Planer Graphs
DEFINITION A graph is called planar if it can be drawn in the plane without any edges crossing (where a crossing of edges is the intersection of the lines or arcs representing them at a point other than their common endpoint). Such a drawing is called a planar representation of the graph. A graph may be planar even if it is usually drawn with crossings, because it may be possible to draw it in a different way without crossings.
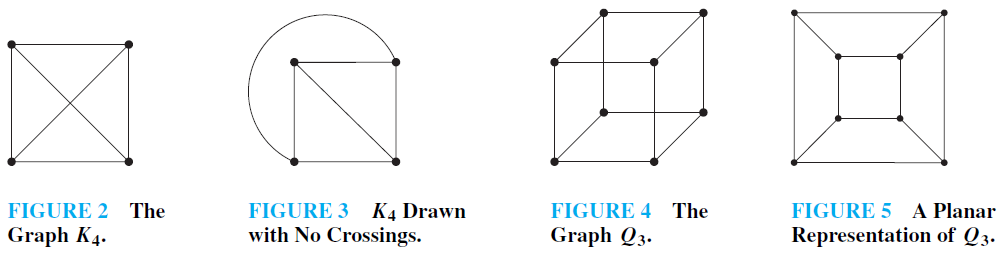
EXAMPLE 1 Is K4 (shown in Figure 2 with two edges crossing) planar?
Solution: K4 is planar because it can be drawn without crossings, as shown in Figure 3.
EXAMPLE 2 Is Q3, shown in Figure 4, planar?
Solution: Q3 is planar, because it can be drawn without any edges crossing, as shown in Figure 5.
We can show that a graph is planar by displaying a planar representation. It is harder to show that a graph is nonplanar.We will give an example to show how this can be done in an ad hoc fashion. Later we will develop some general results that can be used to do this.
EXAMPLE 3 Is K3,3, shown in Figure 6, planar?
Solution: Any attempt to draw K3,3 in the plane with no edges crossing is doomed. We now show why. In any planar representation of K3,3, the vertices v1 and v2 must be connected to both v4 and v5. These four edges form a closed curve that splits the plane into two regions, R1 and R2, as shown in Figure 7(a). The vertex v3 is in either R1 or R2. When v3 is in R2, the inside of the closed curve, the edges between v3 and v4 and between v3 and v5 separate R2 into two subregions, R21 and R22, as shown in Figure 7(b).
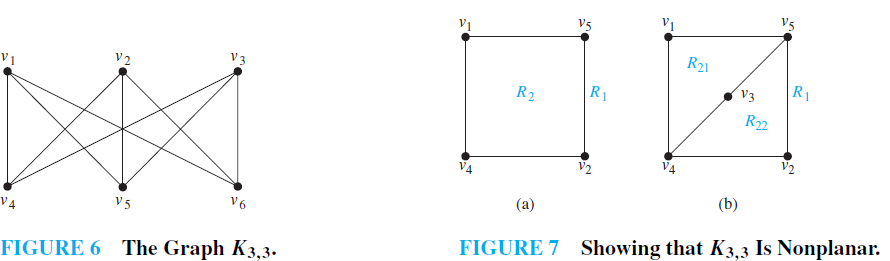
Next, note that there is no way to place the final vertex v6 without forcing a crossing. For if v6 is in R1, then the edge between v6 and v3 cannot be drawn without a crossing. If v6 is in R21, then the edge between v2 and v6 cannot be drawn without a crossing. If v6 is in R22, then the edge between v1 and v6 cannot be drawn without a crossing.
A similar argument can be used when v3 is in R1. The completion of this argument is left for the reader (see Exercise 10). It follows that K3,3 is not planar.
Example 3 solves the utilities-and-houses problem that was described at the beginning of this section. The three houses and three utilities cannot be connected in the plane without a crossing. A similar argument can be used to show that K5 is nonplanar. (See Exercise 11.)
APPLICATIONS OF PLANAR GRAPHS Planarity of graphs plays an important role in the design of electronic circuits.We can model a circuit with a graph by representing components of the circuit by vertices and connections between them by edges. We can print a circuit on a single board with no connections crossing if the graph representing the circuit is planar. When this graph is not planar, we must turn to more expensive options. For example, we can partition the vertices in the graph representing the circuit into planar subgraphs. We then construct the circuit using multiple layers. (See the preamble to Exercise 30 to learn about the thickness of a graph.) We can construct the circuit using insulated wires whenever connections cross. In this case, drawing the graph with the fewest possible crossings is important.
The planarity of graphs is also useful in the design of road networks. Suppose we want to connect a group of cities by roads. We can model a road network connecting these cities using a simple graph with vertices representing the cities and edges representing the highways connecting them.We can built this road network without using underpasses or overpasses if the resulting graph is planar.