Introduction To Lattices
Definition: A lattice is a partially ordered set (L, £) in which every subset {a, b} consisting of two element has a least upper bound and a greatest lower bound. We denote lub({a, b}) by a ∨ b and call it join or sum of a and b. Similarly, we denote GLB({a, b}) by a ∧ b and call it meet or product of a and b.
Other symbol used are:
![]()
Thus Lattice is a mathematical structure with two binary operations, join and meet. Lattice structures often appear in computing and mathematical applications.
A totally ordered set is obviously a lattice but not all partially ordered sets are lattices.
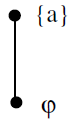
Example 1. Let A be any set and P(A) be its power set. The partially ordered set (P(A), ⊆) is a lattice in which the meet and join are the same as the operations ∪ and ∩ respectively. If A has single element, say a, then P(A) = {φ, {a}} and
![]()
The Hasse diagram of (P(A), ⊆) is a chain containing two elements φ and {a} as shown below:
If A has two elements, say a and b. Then P(A) = {φ, {a}, {b}, {a, b}}. The Hasse diagram of {P(A), ⊆ ) is then as shown below :
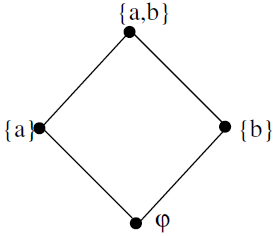
We note that
1. LUB exists for every two subsets and is L ∪ M
2. GLB exists for every two subsets and is in L ∩ M
for L, M ∈ P(A). Hence P(A) in a lattice.
Example 2. Consider the poset (N, ≤), where ≤ is relation of divisibility. Then N is a lattice in which
join of a and b = a ∨ b = L C M(a, b)
meet of a and b = a ∧ b = G C D (a, b) for a, b Î N.
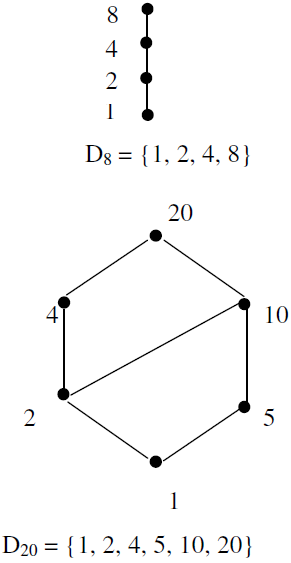
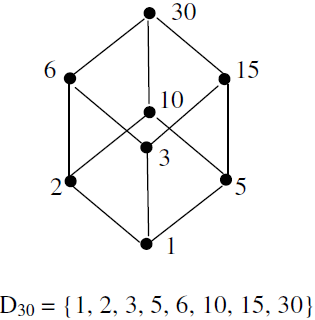
Example 3. Let n be a positive integer and let Dn be the set of all positive divisors of n. Then Dn is a lattice under the relation of divisibility. The Hasse diagram of the lattices D8, D20 and D30 are respectively