Introduction To Partial Order Relations

INTRODUCTION: We often use relation to describe certain ordering on the sets. For example, lexicographical ordering is used for dictionary as well as phone directory. We schedule certain jobs as per certain ordering, such as priority. Ordering of numbers may be in the increasing order.

In the previous chapter, we have discussed various properties (reflexive etc) of relation. In this chapter we use these to define ordering of the sets.

Definition: A relation R on the set A is said to be partial order relation, if it is reflexive, anti-symmetric and transitive. Before we proceed further, we shall have a look at a few examples of partial order relations.
Example : Let A = {a, b, c, d, e}. Relation R, represented using following matrix is a partial order relation.

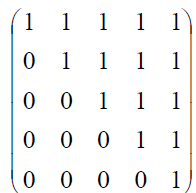
Observe the reflexive, anti-symmetric and transitive properties of the relation from the matrix.

Example : Let A be a set of natural numbers and relation R be “less than or equal to relation (≤)”. Then R is a partial order relation on A. For any m, n, k ≤ N, n ≤ n (reflexive); if m ≤ n and m ≥ n, then m = n (anti-symmetric); lastly, if m ≤ n and n ∈ k, then m ≤ k (transitive).

Definition : If R is a partial order relation on a set A, then A is called as partial order set and it is denoted with (A, R). Typically this set is termed as poset and the pair is denoted with (A, ≤).