Mathematical Induction
MATHEMATICAL INDUCTION: Here we discuss another proof technique. Suppose the statement to be proved can be put in the from nn0. P(n), where n0 is some fixed integer. That is suppose we wish to show that P(n) is true for all integers n ≥ n0.
The following result shows how this can be done. Suppose that
(a) P(n0) is true and
(b) If P(K) is true for some K ≥ n0, then P(K 1) must also be true. The P(n) is true for all n ≥ n0.
This result is called the principle of Mathematical induction. Thus to prove the truth of statement ∀ n≥n0. P(n), using the principle of mathematical induction, we must begin by proving directly that the first proposition P(n0) is true. This is called the basis step of the induction and is generally very easy. Then we must prove that P(K) ∀ P(K 1) is a tautology for any choice of K ≥ n0. Since, the only case where an implication is false is if the antecedent is true and the consequent is false; this step is usually done by showing that if P(K) were true, then P(K 1) would also have to be true.
This step is called induction step: In short we solve by following steps.
1. Show that P(1) is true.
2. Assume P(k) is true.
3. Prove that P(k 1) is true using P(k) Hence P(n) is true for every n.
Example : Using principle of mathematical induction prove that…
1) ![]()
2) n3 - n is divisible by 3 for n ∈ Z
3) 2n > n for all positive integers n.
4) n! ≥ 2n–1
5) If A1, A2,……An be any n sets then ![]()
Solution :
![]()
Step 1 : Here n0 = 1
We must show that P (1) is true.
P (1) is the statement
![]()
Which is clearly true. Hence P(1) is true.
Step 2 : Assume P(K) is true for K ≥ n.
![]()
Step 3 : To show that P(K 1) is true.
![]()
Consider,
![]()
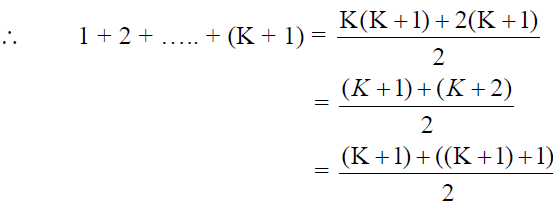
Which is RHS of P(K 1)
Thus, P(K 1) is true.
∴ By principle of mathematical induction it follows that P(n) is true for all n≥1.
∴ 1 2 ….. n = n(n -1)/2
2) Let P(n) : n3 – n is divisible by 3.