Maximal, Minimal Elements And Lattices

MAXIMAL, MINIMAL ELEMENTS AND LATTICES: In this section, we discuss certain element types in the poset and hence a special kind of poset, Lattice.
To understand these types, we shall refer to the following figures, i.e. Fig.4.6 and Fig.4.7.

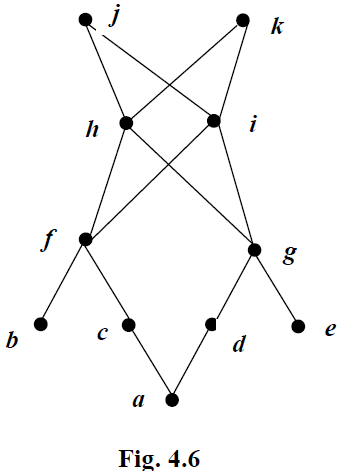
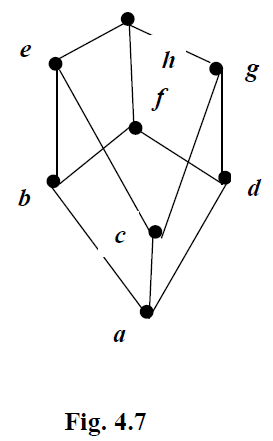
Definition 1: Let (A, ≤) be a poset. An element a ∈ A is called a maximal element, if for no b ∈ A, a ≠ b, a ≤ b. E.g. In Fig. 4.6, j and k are
maximal elements.

Definition 2: Let (A, ≤) be a poset. An element a ∈ A is called a minimal element, if for no b ∈ A, a ≠ b, b ≤ a. E.g. In Fig. 4.6, a, b and e are minimal elements.

Definition 3: Let a, b be two elements in the poset (A, ≤). An element c ∈ A, is said to be an upper bound of a, b if a ≤ c and b ≤  c. E.g. In Fig 4.7, f1 h are upper bounds of b and d.

Definition 4: Let a, b be two elements in the poset (A, ≤). An element c ∈ A, is said to be a least upper bound of a, b if a ≤ c and b ≤ c and if d is an upper bound of a, b, then c ≤ d. E.g. In Fig 2.7, f is a least upper bound of b and d.

Definition 5: Let a, b be two elements in the poset (A, ≤). An element c ∈ A, is said to be a lower bound of a, b if c ≤ a and c ≤ b. E.g. In Fig 4.6, f, g are lower bounds of h and i.

Definition 6: Let a, b be two elements in the poset (A, ≤). An element c ∈ A, is said to be a greatest lower bound of a, b if c ≤ a and c ≤ b and if d is a lower bound of a, b, then d ≤ c. E.g. In Fig 4.7, c is a greatest lower bound of e and g.

Definition 7: A poset (A, ≤) is said to be a lattice, if every two elements in A have a unique least upper bound and a unique greatest lower bound.
E.g. Fig. 4.6 is not a lattice, because j and k are two least upper bounds of h and i, whereas Fig. 4.7 is a lattice.