Method Of Solving Recurrence Relation

METHODS OF SOLVING RECURRENCE RELATION: Now, in this section we shall discuss a few methods of solving recurrence relation and hence solve the relations that we have formulated in the Recurrence Relation section.

Backtracking Method: This is the most intuitive way of solving a recurrence relation. In this method, we substitute for every term in the sequence in the form of previous term (i.e. an in the form of a_n–1, a_n–1 in the form of a_n–2 and so on) till we reach the initial condition and then substitute for the initial condition. To understand this better, we shall solve the recurrence relations that we have come across earlier.
Example: Solve the recurrence relation in a_n = 1.06a_n–1, with a₀ = 0.5.
Solution: Given recurrence relation is an = 1.06a_n–1, with a₀ = 0.5. From this equation, we have a_n = 1.06a_n–1 = 1.06 ≥ 1.06 an–2 = 1.06 ≥ 1.06 ≥ 1.06 an–3
Proceeding this way, we have a_n = (1.06)na₀. But, we know that a₀ = 0.5.
Thus, explicit solution to the given recurrence relation is an = 0.5 ≥ (1.06)n for n ≥ 0.
Example : Solve the Tower of Hanoi puzzle, using backtracking method.
Solution: The recurrence relation, for the puzzle is:
H_n = 1 if n = 1.
H_n = 2H_n–1 1 otherwise.

Thus, Hn = 2H_n–1 1 = H_n = 2 X (H_n–2 1) 1 = 2²H_n–2 2 1 = 2² (2H_n–3 1 ) 2 1 = 2³H_n–3 2² 2 1. Proceeding this way, we have

H_n = 2^n–1H₁ 2^n–2 2^n–3 2^n–4 ... 1.
= 2^n–1 2^n–2 2^n–3 2^n–4 ... 1 (H₁ = 1)
= 2^{n – 1}.
Example : Find the recurrence relation to count the number of regions created by n lines in a plane, such that each pair of lines has exactly one
point of intersection. Solve this recurrence relation.

Solution: Let rn be the number of regions created by n lines following the condition mentioned in the example. If the number of lines is 1, then obviously, r₁ = 2. If number of lines is 2, then r₂ = 4. Now, we shall assume that there are n–1 lines satisfying the condition mentioned. Then the number of regions created by these lines is r_n–1. If we add one more line, that interest each of these line exactly once then n more regions are created as follows:

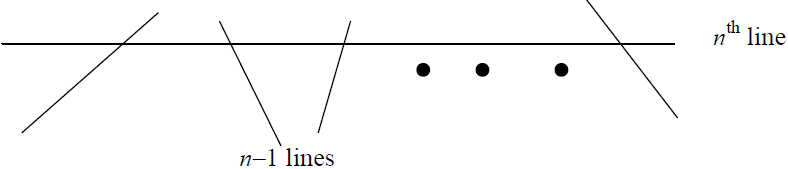
Then, as we observe from above diagram, if nth line intersects all n–1 lines, then new n regions are created. Thus, the recurrence relation is:

r_n = r_n–1 n, with r₁ = 2.
To solve this equation, we shall use the backtracking method.
r_n = r_n–1 n = (r_n–1 n – 1) n = ... = r₁ 2 3 ... n = 1 2 3 ... n 1 = 1 n(n 1)/2