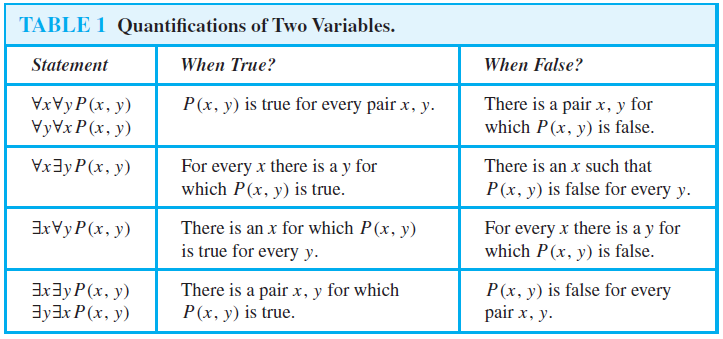
Nested Quantifiers

Example 4 illustrates that the order in which quantifiers appear makes a difference. The statements ∃y∀xP(x, y) and ∀x∃yP(x, y) are not logically equivalent. The statement ∃y∀xP(x, y) is true if and only if there is a y that makes P(x, y) true for every x. So, for this statement to be true, there must be a particular value of y for which P(x, y) is true regardless of the choice of x. On the other hand, ∀x∃yP(x, y) is true if and only if for every value of x there is a value of y for which P(x, y) is true. So, for this statement to be true, no matter which x you choose, there must be a value of y (possibly depending on the x you choose) for which P(x, y) is true. In other words, in the second case, y can depend on x, whereas in the first case, y is a constant independent of x.
From these observations, it follows that if ∃y∀xP(x, y) is true, then ∀x∃yP(x, y) must also be true. However, if ∀x∃yP(x, y) is true, it is not necessary for ∃y∀xP(x, y) to be true.

EXAMPLE 5 Let Q(x, y, z) be the statement “x y = z.” What are the truth values of the statements ∀x∀y∃zQ(x, y, z) and ∃z∀x∀yQ(x, y, z), where the domain of all variables consists of all real numbers?
Solution: Suppose that x and y are assigned values. Then, there exists a real number z such that x y = z. Consequently, the quantification
∀x∀y∃zQ(x, y, z),
which is the statement
“For all real numbers x and for all real numbers y there is a real number z such that x y = z,”

is true. The order of the quantification here is important, because the quantification
∃z∀x∀yQ(x, y, z),
which is the statement
“There is a real number z such that for all real numbers x and for all real numbers y it is true that x y = z,” is false, because there is no value of z that satisfies the equation x y = z for all values of x and y.