Normal Form Of A Well Formed Formula

Normal Form of a well formed formula : One of the main problem in logic is to determine whether the given statement is a tautology or a contradiction. One method to determine it is the method of truth tables. Other method is to reduce the statement form to, called normal form.
If P & Q are two propositional variables we get various well formed formula.
The number of distinct truth values for formulas in P and Q is 2⁴.

Thus there are only 16 distinct formulae & any formula in P & Q is equivalent to one of these formulas.
Here we give a method of reducing a given formula to an equivalent form called a ‘normal form’. We use ‘sum’ for disjunction, ‘product’ for conjunction and ‘literal’ either for P or for ¬ P , where P is any propositional variable.

Elementary Sum & Elementary Product : An elementary sum is a sum of literals. An elementary product is a product of literals.
e.g. P ∨ ¬ Q, P ∨ ¬ R are elementary sum P ∧ ¬ Q, ¬ P ∧ Q are elementary products.

Disjunctive Normal Form (DNF) : A formula is in disjunctive normal form if it is a sum of elementary products.

A conjunction of statement variables and their negations are called as fundamental conjunctions. It is also called min term.

Construction to obtain a Disjunctive Normal Form of a given formula

The following procedure is used to obtain a disjunctive normal form.
1. Eliminate → and ⇔ using logical identifies.
2. Use De-Morgans laws to eliminate ¬ before sums or products. The resulting formula has ¬ only before propositional variables i.e. it involves sum, product and literals.
3. Apply distributive laws repeatedly to eliminate product of sums. The resulting formula will be sum of products of literals i.e. sum of elementary products.

Example : Obtain a disjunctive normal form of

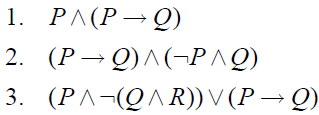
Answer :
1) Consider, P ∧ (P → Q)
≡ P∧( ¬ P ∨ Q) (Implication law)
(P∧ ¬ P) ∨ (P ∧ Q) (Distributive law)
This is a disjunctive normal form of the given formula.
2) Using Implication law

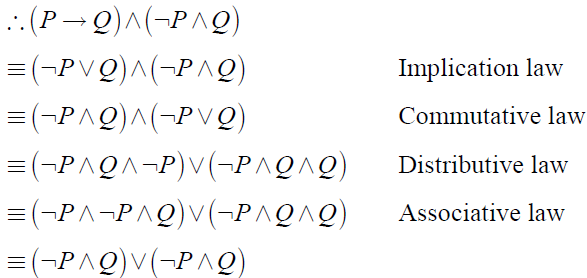
This is required disjunctive normal form

3) 

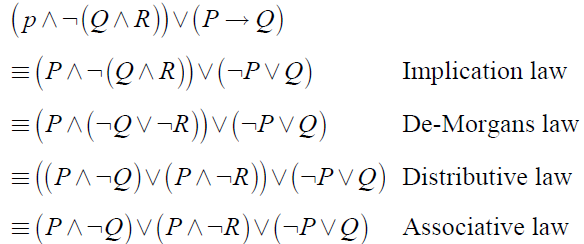
This is the disjunctive normal form of the given formula.

• Note that for the same formula we may get different disjunctive normal forms. So we introduce one or more normal forms called the principle disjunctive normal form or sum of products canonical form in the next definition. The advantage of constructing principle disjunctive normal form is that for a given formula principle disjunctive normal form is unique.
• Two forms are said to be equivalent iff their principle disjunctive normal forms consider.

* Min term : A min term in n propositional variables P1, P2, ……, Pn is Q1 ∧Q2 ∧......... ∧Qn where each Qi is either Pi or ¬ Pi.
e.g. The min terms in P1 & P2 are P1 ∧ P2, P1 ∧ ¬ P2, ¬ P1 ∧ P2, ¬ P1 ∧ ¬ P2, In general the number of min terms in n propositional variables is 2ⁿ.