Octal Number System
Octal number system: Octal system was used to deal with the long strings of 1s and 0s in binary. It is a base 8 system using the digits 0, 1, 2, 3, 4, 5, 6 and 7. Thus each digit of an octal number can have only values 0 to 7. The digit position in an octal number have weights as follows-
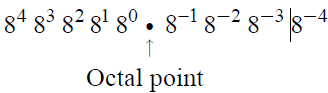
The largest octal digit is 7. After 7, the next digit is taken to be 10.
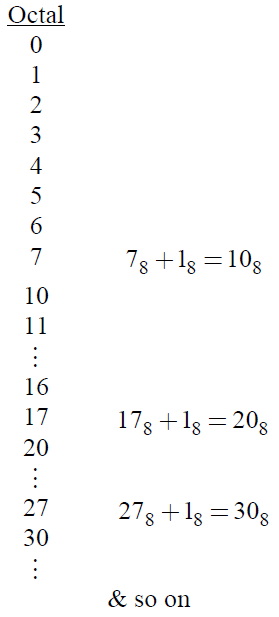
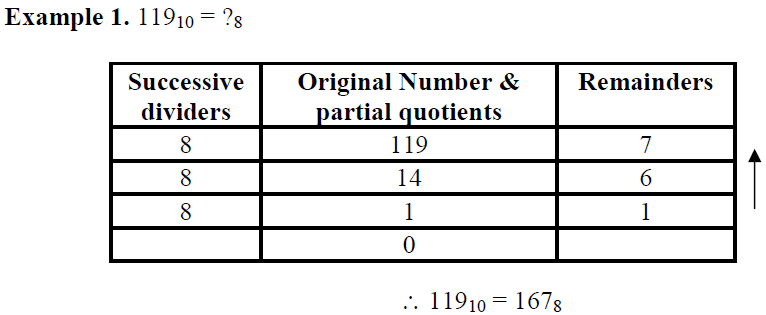
Decimal to Octal conversion:
Steps:
1) Divide the decimal number by 8.
2) Place the remainder to the right of original number.
3) Subsequently divide the partial quotient by 8 and place the remainder to the right of partial quotient.
4) Repeat the above steps till we get partial quotient 0.
5) The octal number is equal to the remainder arranged so that first remainder is LSD and last remainder is MSD of the octal number (i.e. from down to up)
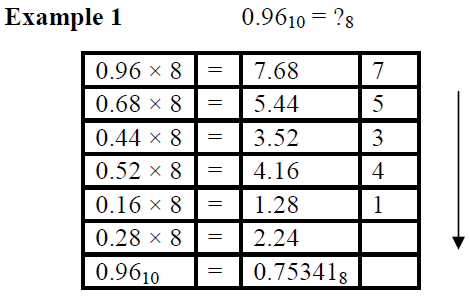
Decimal to Octal fraction Conversion :
Steps:
1) Multiply the decimal fraction by 8.
2) Write the integer to the right of the product i.e. if 0.6 x 8 = 4.8 then place 4 to the right of the product.
3) The partial product is again multiplied by 8 and the integer is placed to the right of the product.
4) Repeat the process till the partial products is seen or till the required place of octal point.
Octal Decimal Conversion : To convert a whole octal number to its decimal equivalent, the extreme right hand digit is multiplied by 80, the second digit from right is multiplied by 81, the third from right is multiplied by 82, and so on. Then all their products are added to get the required decimal number.
To convert octal fraction to decimal fraction- Multiply first digit after octal point by 8-1, second digit after octal point by 8-2, third digit after octal point by 8-3 & so on. Add all their products to get the required decimal fraction.
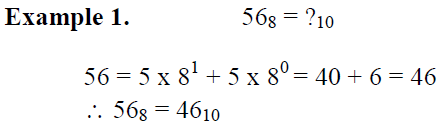
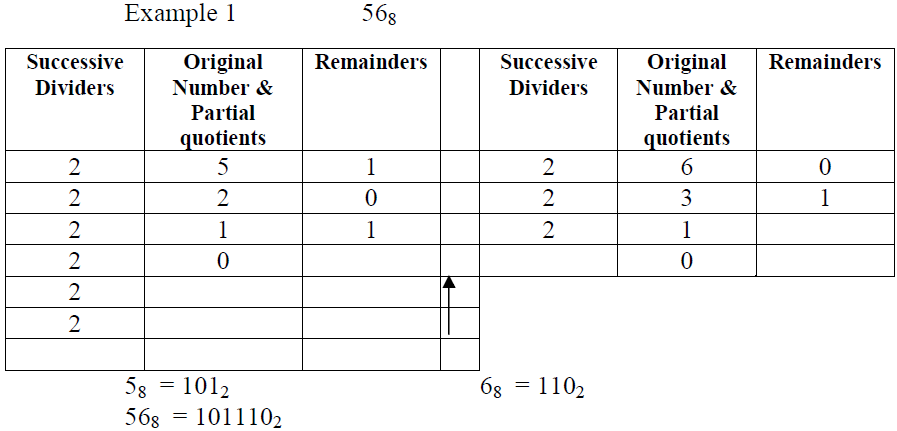
Octal to Binary Conversion: The conversion of octal to binary is done by converting each octal digit to its 3-bit binary equivalent