Principle Disjunctive Normal Form
Principle Disjunctive Normal Form : A formula α is in principle disjunctive normal form if α is a sum of min terms. Steps to Construct Principle Disjunctive Normal Form of a given Formula : -
1. First obtain the disjunctive normal form for given formula.
2. Drop elementary products, which are contradiction such as (P∧ ¬ P)
3. If Pi & ¬ Pi are not present in an elementary product α , replace α by ![]()
4. Use the above step until all elementary products are reduced to sum of min terms.
Use idempotent laws to avoid repetition of min terms.
Example : Obtain the canonical sum of product form i.e. principle disjunctive normal form of
1. ![]()
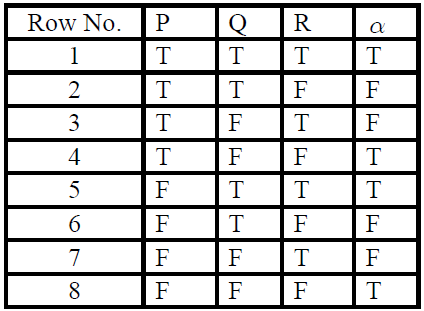
2. α whose truth table is given below
Answer :
1) α is already in disjunctive normal form. There are no contradictions. So we have to introduce missing - variables. PQ R in is a min - term.
![]()
![]()
Therefore the canonical sum of products form of α is
![]()
2) For given α , we have T in column corresponding to rows 1, 4, 5 and 8. The min terms corresponding to these rows are
![]()
The principle disjunctive normal form of α is
![]()
Fundamental disjunction (Max term): A disjunction of statement variables and (or) their negations are called as fundamental disjunctions. It is also called max term.
![]()
Conjunctive Normal Form : - A statement form which consists of a conjunction of a fundamental disjunction is called a conjunctive normal form.
![]()
Maxterm: A max term in n propositional variables P1, P2 , ....... Pn is Q1 ∨ Q2 ∨........... ∨Qn where each Qi is either Pi or ¬ p