Representation Of Relations
REPRESENTATION OF RELATIONS: Matrices and graphs are two very good tools to represent various algebraic structures. Matrices can be easily used to represent relation in any programming language in computer. Here we discuss the representation of relation on finite sets using these tools. Consider the relation in Example 3.1.
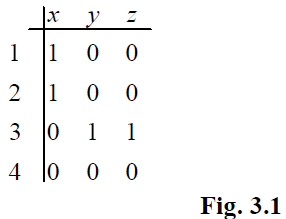
Thus, if a R b, then we enter 1 in the cell (a, b) and 0 otherwise. Same relation can be represented pictorially as well, as follows:
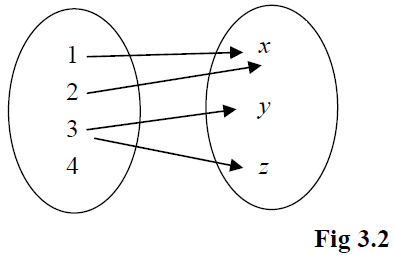
Thus, two ovals represent sets A and B respectively and we draw an arrow from a ∈ A to b ∈ B, if a R b.
If the relation is from a finite set to itself, there is another way of pictorial representation, known as diagraph.
For example, let A = {1, 2, 3, 4} and R be a relation from A to itself, defined as follows:
R = {(1, 2), (2, 2), (2, 4), (3, 2), (3, 4), (4, 1), (4, 3)}
Then, the diagraph of R is drawn as follows:
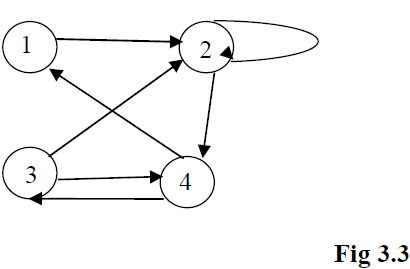
The directed graphs are very important data structures that have applications in Computer Science (in the area of networking).
Definition: Let A, B and C be three sets. Let R be a relation from A to B and S be a relation from B to C. Then, composite relation R0S, is a relation from A to C, defined by, a(R0S)c, if there is some b ∈ B, such that a R b and b bsc.
Example : Let A = {1, 2, 3, 4}, B = {a, b, c, d}, C = {x, y, z } and let R = {(1, a), (2, d), (3, a), (3, b), (3, d)} and S = {(b, x), (b, z), (c, y), (d, z)}.
Pictorial representation of the relation in Example 3.6 can be shown as below (Fig 3.4).
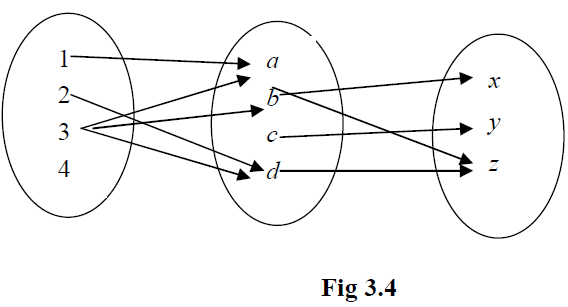
Thus, from the definition of composite relation and also from Fig 3.4, R0S will be given as below. R0S = {(2, z), (3, x), (3, z)}.
There is another way of finding composite relation, which is using matrices.
Example : Consider relations R and S in above example. Their matrix representations are as follows.
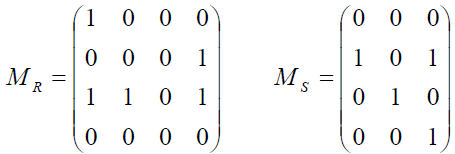
Consider the product of matrices MR and MS as follows:
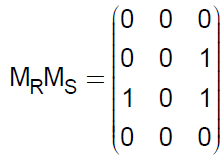
Observe that the non-zero entries in the product tell us which elements are related in R0S. Hence, MRMS and MR0S have same non-zero entries.