Rules Of Inference For Propositional Logic

Rules of Inference for Propositional Logic: We can always use a truth table to show that an argument form is valid.We do this by showing that whenever the premises are true, the conclusion must also be true. However, this can be a tedious approach. For example, when an argument form involves 10 different propositional variables, to use a truth table to show this argument form is valid requires 210 = 1024 different rows. Fortunately, we do not have to resort to truth tables. Instead, we can first establish the validity of some relatively simple argument forms, called rules of inference. These rules of inference can be used as building blocks to construct more complicated valid argument forms. We will now introduce the most important rules of inference in propositional logic. The tautology (p ∧ (p → q)) → q is the basis of the rule of inference called modus ponens, or the law of detachment. (Modus ponens is Latin for mode that affirms.) This tautology leads to the following valid argument form, which we have already seen in our initial discussion about arguments (where, as before, the symbol ∴ denotes “therefore”):
p
p → q
∴ q
Using this notation, the hypotheses are written in a column, followed by a horizontal bar, followed by a line that begins with the therefore symbol and ends with the conclusion. In particular, modus ponens tells us that if a conditional statement and the hypothesis of this conditional statement are both true, then the conclusion must also be true. Example 1 illustrates the use of modus ponens.

EXAMPLE 1 Suppose that the conditional statement “If it snows today, then we will go skiing” and its hypothesis, “It is snowing today,” are true. Then, by modus ponens, it follows that the conclusion of the conditional statement, “We will go skiing,” is true.
As we mentioned earlier, a valid argument can lead to an incorrect conclusion if one or more of its premises is false.We illustrate this again in Example 2.

EXAMPLE 2 Determine whether the argument given here is valid and determine whether its conclusion must
be true because of the validity of the argument.

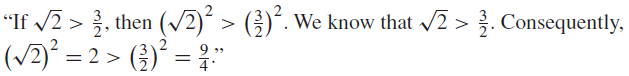
Solution: Let p be the proposition “
√2 > 3/2 ” and q the proposition “2 > (3/2 )2.” The premises of the argument are p → q and p, and q is its conclusion. This argument is valid because it is constructed √ by using modus ponens, a valid argument form. However, one of its premises, 2 > 3/2 , is false. Consequently, we cannot conclude that the conclusion is true. Furthermore, note that the conclusion of this argument is false, because 2 < 9/4 .

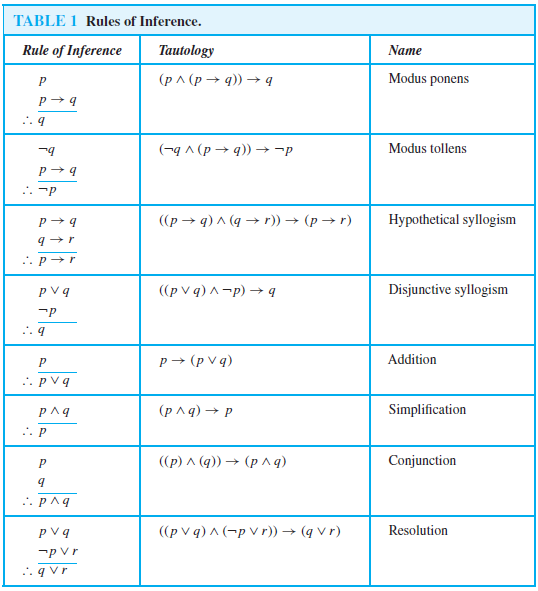
There are many useful rules of inference for propositional logic. Perhaps the most widely used of these are listed in Table 1. We now give examples of arguments that use these rules of inference. In each argument, we first use propositional variables to express the propositions in the argument. We then show that the resulting argument form is a rule of inference from Table 1.

EXAMPLE 3 State which rule of inference is the basis of the following argument: “It is below freezing now. Therefore, it is either below freezing or raining now.”
Solution: Let p be the proposition “It is below freezing now” and q the proposition “It is raining now.” Then this argument is of the form
p
∴ p ∨ q
This is an argument that uses the addition rule.

EXAMPLE 4 State which rule of inference is the basis of the following argument: “It is below freezing and raining now. Therefore, it is below freezing now.”
Solution: Let p be the proposition “It is below freezing now,” and let q be the proposition “It is raining now.” This argument is of the form
p ∧ q
∴ p
This argument uses the simplification rule.