Trees As Models
Trees as Models: Trees are used as models in such diverse areas as computer science, chemistry, geology, botany, and psychology.We will describe a variety of such models based on trees.
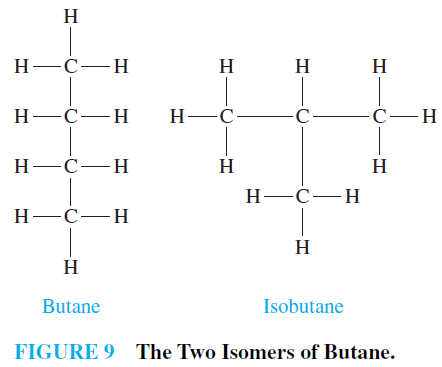
EXAMPLE 5 Saturated Hydrocarbons andTrees Graphs can be used to represent molecules, where atoms are represented by vertices and bonds between them by edges. The English mathematicianArthur Cayley discovered trees in 1857 when he was trying to enumerate the isomers of compounds of the form CnH2n 2, which are called saturated hydrocarbons.
In graph models of saturated hydrocarbons, each carbon atom is represented by a vertex of degree 4, and each hydrogen atom is represented by a vertex of degree 1. There are 3n 2 vertices in a graph representing a compound of the form CnH2n 2. The number of edges in such a graph is half the sum of the degrees of the vertices. Hence, there are (4n 2n 2)/2 = 3n 1 edges in this graph. Because the graph is connected and the number of edges is one less than
the number of vertices, it must be a tree.
The nonisomorphic trees with n vertices of degree 4 and 2n 2 of degree 1 represent the different isomers of CnH2n 2. For instance, when n = 4, there are exactly two nonisomorphic trees of this type (the reader should verify this). Hence, there are exactly two different isomers
of C4H10. Their structures are displayed in Figure 9. These two isomers are called butane and
isobutane.
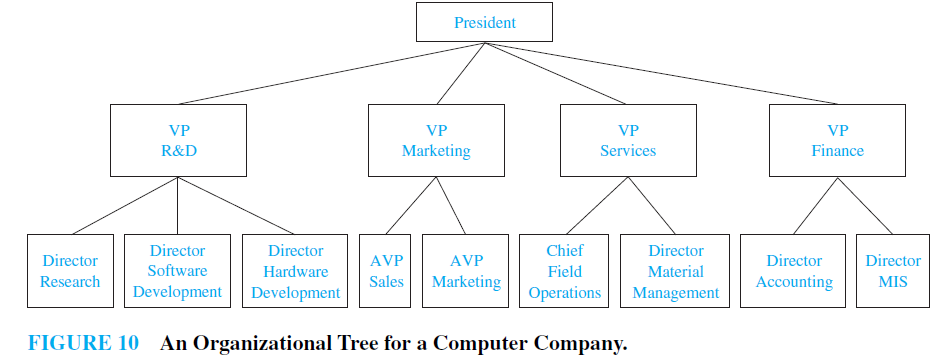
EXAMPLE 6: Representing Organizations The structure of a large organization can be modeled using a rooted tree. Each vertex in this tree represents a position in the organization. An edge from one vertex to another indicates that the person represented by the initial vertex is the (direct) boss of the person represented by the terminal vertex. The graph shown in Figure 10 displays such a tree. In the organization represented by this tree, the Director of Hardware Development works directly for the Vice President of R&D.
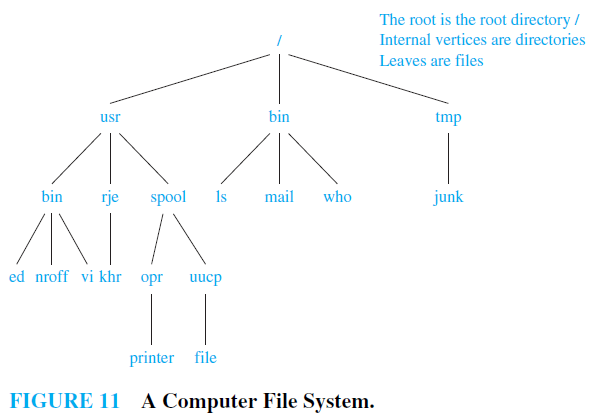
EXAMPLE 7 Computer File Systems Files in computer memory can be organized into directories. A directory can contain both files and subdirectories. The root directory contains the entire file
system. Thus, a file system may be represented by a rooted tree, where the root represents the root directory, internal vertices represent subdirectories, and leaves represent ordinary files or empty directories. One such file system is shown in Figure 11. In this system, the file khr is in the directory rje. (Note that links to files where the same file may have more than one pathname can lead to circuits in computer file systems.)
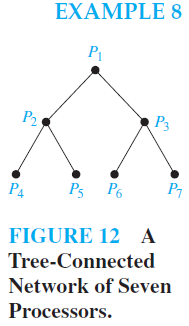
Tree-Connected Parallel Processors In Example 17 of Section 10.2 we described several interconnection networks for parallel processing.A tree-connected network is another important way to interconnect processors. The graph representing such a network is a complete binary tree, that is, a full binary tree where every root is at the same level. Such a network interconnects n = 2k − 1 processors, where k is a positive integer. A processor represented by the vertex v that is not a root or a leaf has three two-way connections—one to the processor represented by the parent of v and two to the processors represented by the two children of v. The processor represented by the root has two two-way connections to the processors represented by its two children.A processor represented by a leaf v has a single two-way connection to the parent of v. We display a tree-connected network with seven processors in Figure 12.
We now illustrate how a tree-connected network can be used for parallel computation. In particular, we show how the processors in Figure 12 can be used to add eight numbers, using three steps. In the first step, we add x1 and x2 using P4, x3 and x4 using P5, x5 and x6 using P6, and x7 and x8 using P7. In the second step, we add x1 x2 and x3 x4 using P2 and x5 x6 and x7 x8 using P3. Finally, in the third step, we add x1 x2 x3 x4 and x5 x6 x7 x8 using P1. The three steps used to add eight numbers compares favorably to the seven steps required to add eight numbers serially, where the steps are the addition of one number to the sum of the previous numbers in the list.