Truth Tables Of Compound Propositions
Truth Tables of Compound Propositions
We have now introduced four important logical connectives—conjunctions, disjunctions, conditional statements, and biconditional statements—as well as negations.We can use these connectives to build up complicated compound propositions involving any number of propositional variables.We can use truth tables to determine the truth values of these compound propositions, as Example 1 illustrates. We use a separate column to find the truth value of each compound expression that occurs in the compound proposition as it is built up. The truth values of the compound proposition for each combination of truth values of the propositional variables in it is found in the final column of the table.
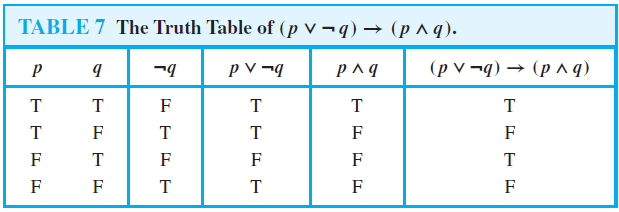
EXAMPLE 1 Construct the truth table of the compound proposition
(p ∨¬q) → (p ∧ q).
Solution: Because this truth table involves two propositional variables p and q, there are four rows in this truth table, one for each of the pairs of truth values TT, TF, FT, and FF. The first two columns are used for the truth values of p and q, respectively. In the third column we find the truth value of ¬q, needed to find the truth value of p ∨¬q, found in the fourth column. The fifth column gives the truth value of p ∧ q. Finally, the truth value of (p ∨¬q) → (p ∧ q) is found in the last column. The resulting truth table is shown in Table 7.