←
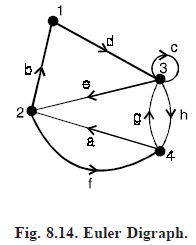
Graph Theory
Arborescence
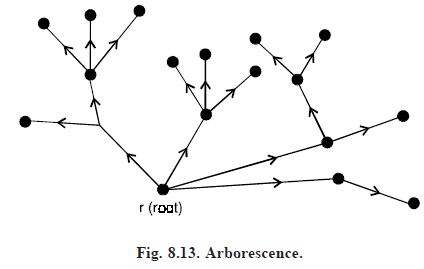
ARBORESCENCE: A digraph G is said to be an arborescence if
(i) G contains no circuit, neither directed nor semi circuit.
(ii) In G there is precisely one vertex v of zero in-degree.
This vertex v is called the root of the arborescence. An arborescence is shown in Fig. 8.13 below.
Spanning arborescence: A spanning tree in an n-vertex connected digraph, analogous to a spanning tree in an undirected graph, consists of n – 1 directed edges.
A spanning arborescence in a connected digraph is a spanning tree that is an arborescence.
For example, a spanning arborescence in Fig. 8.14, is {f, b, d}. There is a striking relationship between a spanning arborescence and an Euler line.