Binary Search Tree

BINARY SEARCH TREES
A binary search tree is basically a binary tree, and therefore it can be traversed in preorder postorder, and inorder. If we traverse a binary search tree in inorder and print the identifiers contained in the vertices of the tree, we get a sorted list of identifiers in the ascending order. Binary trees are used extensively in computer science to store elements from an ordered set such as a set of numbers or a set of strings. Suppose we have a set of strings and numbers. We call them as keys. We are interested in two of the many operations that can performed on this set.

(i) ordering (or sorting) the set
(ii) searching the ordered set to locate a certain key and, in the event of not finding the key in the set, adding it at the right position so that the ordering of the set is maintained.
A binary search tree is a binary tree T in which data are associated with the vertices. The data are arranged so that, ∈ for each vertex v in T, each data item in the left subtree of v is less than the data item in v and each data item in the right subtree of v is greater than the data item in v. Thus, a binary search tree for a set S is a label binary tree in which each vertex v is labelled by an element l(v) ∈ S such that

(i) for each vertex u in the left subtree of v, l(u) < l(v),
(ii) for each vertex u in the right subtree of v, l(u) > l(v),
(iii) for each element a ∈ S, there is exactly one vertex v such that l(v) = a.

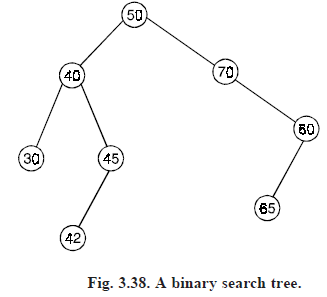
The binary tree T in Fig. 3.38. is a binary search tree since every vertex in T exceeds every number in its left subtree and is less than every number in its right subtree.

Creating a binary search tree
The following recursive procedure is used to form the binary search tree for a list of items. To start, we create a vertex and place the first item in the list in this vertex and assign this as the key of the root. To add a new item, first compare it with the keys of vertices already in the tree. Starting at the root and moving to the left if the item is less than the key of the respective vertex if this has a left child, or moving to the right if the item is greater than the key of the respective vertex if this vertex has a right child when the item is less than the respective vertex and this vertex has no left child, then a new vertex with this item as its key is inserted as a new left child.

Similarly, when the item is greater than the respective vertex and this vertex has no right child, then a new vertex with this item as its key is inserted as a new right child. In this way, we store all the items in the list in the tree and thus create a binary search tree.