Binary Tree
BINARY TREES: A binary tree is a rooted tree where each vertex v has atmost two subtrees ; if both subtrees are present, one is called a left subtree of v and the other right-subtree of v. If only one subtree is present, it can be designated either as the left subtree or right subtree of v. In other words, a binary tree is a 2-ary tree in which each child is designated as a left child or right child. In a binary tree e very vertex has two children or no children.
Full Binary Tree A binary tree is said to be full if each node has either zero or two children. The example here is a full binary tree.
Here is an example of a binary tree that is not full. Notice the nodes with only one child.
There is a relationship between the tree height and the maximum number of terminal nodes. That relationship is:
Maximum terminal nodes = 2tree height
Thus, the maximum number of terminal nodes of a binary tree with a height of 4 would be 16 (=24). Information in trees can be just about anything we can think of. Terminal nodes may be data items, while internal nodes are simply used as connectors. When using binary trees it is not unusual to use the internal nodes as events, which produce new results. An example is a tournament tree (yet another direction for a tree to travel – sideways).
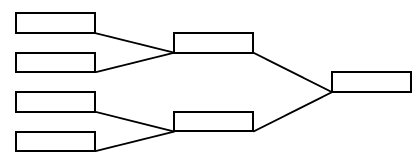
Each internal node creates a new winner which meets the winner of the adjacent contest. The root, then, is the tournament winner.
Properties : (Binary trees) :
(1) The number of vertices n in a complete binary tree is always odd. This is because there is exactly one vertex of even degree, and remaining n – 1 vertices are of odd degree. Since from theorem (i.e., the number of vertices of odd degree is even), n – 1 is even. Hence n is odd.
(2) Let P be the number of end vertices in a binary tree T. Then n – p – 1 is the number of vertices of degree 3. The number of edges in T is
![]() .................(1)
.................(1)
(3) A non end vertex in a binary tree is called an internal vertex. It follows from equation (1) that the number of internal vertices in a binary is one less than the number of end vertices.
(4) In a binary tree, a vertex vi is said to be at level li if vi is at a distance li from the root. Thus the root is at level O.
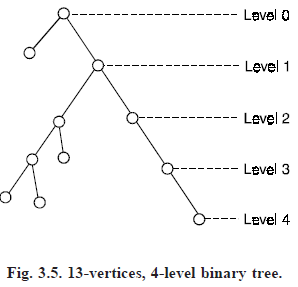
The maximum numbers of vertices possible in a k-level binary tree is 20 21 22 ..... 2k ≥ n, The maximum level, lmax of any vertex in a binary tree is called the height of the tree. On the other hand, to construct a binary tree for a given n such that the farthest vertex is as for as possible from the root, we must have exactly two vertices at each level, except at the O level.