Centroid

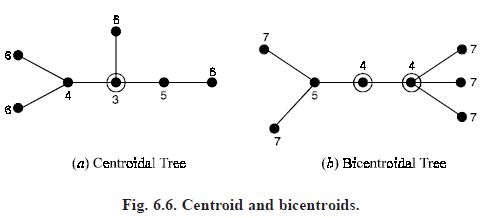
CENTROID: In a tree T, at any vertex v of degree d, there are d subtrees with only vertex v in common. The weight of each subtree at v is defined as the number of branches in the subtree. Then the weight of the vertex v is defined as the weight of the heaviest of the subtrees at v. A vertex with the smallest weight in the entire tree T is called a centroid of T.

Every tree has either one centroid or two centroids. If a tree has two centroids, the centroids are adjacent.

In Fig. 6.6 below, a tree with centroid, called a centroidal tree, and a tree with two centroids, called a bicentroidal tree. The centroids are shown enclosed in circles, and the numbers next to the vertices are the weights.