Colour Problem

COLOUR PROBLEM

• The most famous unsolved problem in graph theory and perhaps in all of Mathematics is the celebrated four colour conjecture. This remarkable problem can be explained in five minutes by any mathematician to the socalled man in the steet. At the end of the explanation, both will understand the problem, but neither will be able to solve it.
• The conjecture states that, any map on a plane or the surface of a sphere can be coloured with only four colours so that no two adjacent countries have the same colour. Each country must consist of a single connected region, and ajdacent countries are those having a boundary line in common. The conjecture has acted as a catalyst in the branch of mathematics known as combinatorial topology and is closely related to the currently fashionable field of graph theory. More than half a century of work by many mathematicians has yielded proofs for special cases ..... . The consensus is that the conjecture is correct but unlikely to be proved in general.
• It seems destined to retain for some time the distinction of being both the simplest and most fascinating unsolved problem of mathematics.
• The four colour conjecture has an interesting history, but its origin remains some what vague. There have been reports that Möbius was familiar with this problem in 1840, but it is only definite that the problem was communicated to De Morgan by Guthrie about 1850.
• The first of many erroneous proofs of the conjecture was given in 1879 by Kempe. An error was found in 1890 by Heawood who showed, however, that the conjecture becomes true when ‘four’ is replaced by ‘five’.
• A counter example, if ever found, will necessarily be extremely large and complicated, for the conjecture was proved most recently by Ore and Stemple for all maps with fewer than 40 countries.

The four colour conjecture is a problem in graph theory because every map yields a graph is which the countries are the points, and two points are joined by a line whenever the corresponding countries are adjacent. Such a graph obviously can be drawn in the plane without intersecting lines. Thus, if it is possible to colour the points of every planar graph with four or fewer colours so that adjacent points have different colours, then the four colour conjecture will have been proved.

The Four colour theorem : Every planar graph is 4-colorable.
Assume the four colour conjecture holds and let G be any plane map.
Let G* be the underlying graph of the geometric dual of G.
Since two regions of G are adjacent if and only if the corresponding vertices of G* are adjacent, map G is 4-colorable because graph G* is 4-colorable.
Conversely, assume that every plane map is 4-colorable and let H be any planar graph.
Without loss of generality, we suppose H is a connected plane graph.
Let H* be the dual of H, so drawn that each region of H* encloses precisely one vertex of H. The connected plane pseudograph H* can be converted into a plane graph H′ by introducing two vertices into each loop of H* and adding a new vertex into each edge in a set of multiple edges.
The 4-colorability of H′ now implies that H is 4-colorable, completing the verification of the equivalence.
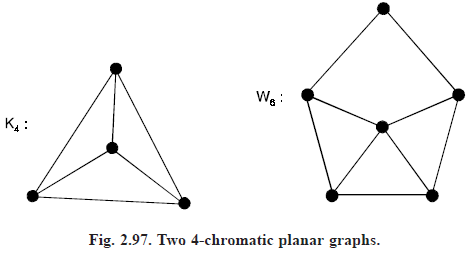
If the four color conjecture is ever proved, the result will be best possible, for it is easy to give examples of planar graphs which are 4-chromatic, such as K4 and W6 (see Figure 2.97 below).

Theorem. The four colour conjecture holds if and only if every cubic bridgeless plane map is 4-colourable.
Proof. We have already seen that every plane map is 4-colourable if and only if the four colour conjecture holds.
This is also equivalent to the statement that every bridgeless plane map is 4-colourable since the elementary contraction of identifying the end vertices of a bridge affects neither the number of regions in the map nor the adjacency of any of the regions.

Certainly, if every bridgeless plane map is 4-colorable, then every cubic bridgeless plane map is 4-colorable.

In order to verify the converse, let G be a bridgeless plane map and assume all cubic bridgeless plane maps are 4-colourable.
Since G is bridgeless, it has no end vertices.
If G contains a vertex v of degree 2 incident with edges y and z, we subdivide y and z, denoting the subdivision vertices by u and w respectively.

We now remove v, identify u with one of the vertices of degree 2 in a copy of the graph K4 – x and identify w with the other vertex of degree 2 in K4 – x.
Observe that each new vertex added has degree 3 (see Figure 2.98). If G contains a vertex v0 of degree n ≥ 4 incident with edges x1, x2, ...... xn, arranged cyclically about v0, we subdivide each xi producing a new vertex vi.

We then remove v0 and add the new edges v1v2, v2v3, ......, vn – 1vn, vnv1. Again each of the vertices so added has degree 3.

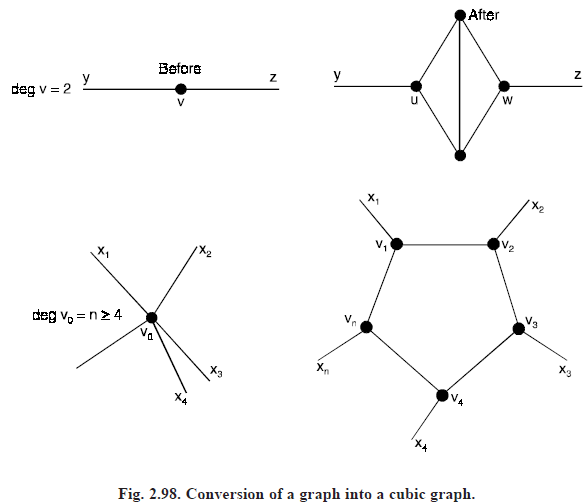
Denote the resulting bridgeless cubic plane map by G′, which, by hypothesis, is 4-colourable. If for each vertex v of G with deg v ≠ 3, we identify all the newly added vertices associated with v in the formation of G′, we arrive at G once again. Thus, let there be given a 4-colouring of G′.

The above mentioned contradiction of G′ into G induces an m-colouring of G, m ≤ 4, which completes the proof.