Complete Binary Tree

COMPLETE BINARY TREE
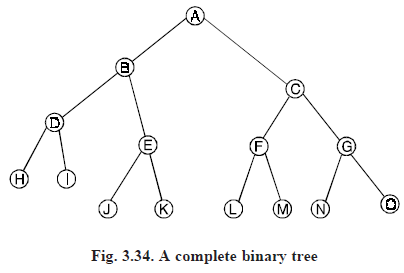
If all the leaves of a full binary tree are at level d, then we call a tree as a complete binary tree of depth d. A complete binary tree of depth of 3 is shown in Fig. (3.34).

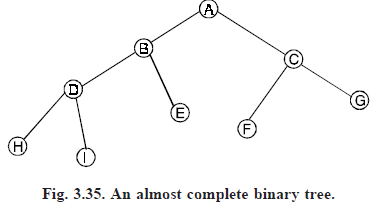
Almost complete binary tree: A binary tree of depth d is said to be almost complete binary tree if
(i) each node in the tree is either at level d or d – 1.
(ii) for any node in the tree with a right descendant at level d, all the left descendants of this node are also at level d.

Fig. (3.35) shows as almost complete binary tree.

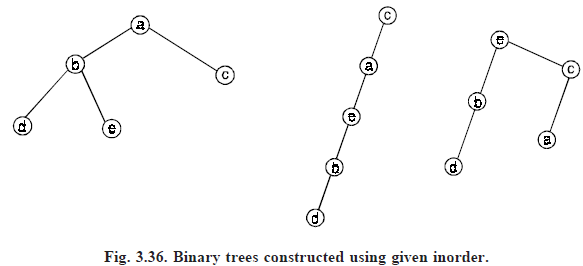
Therefore we can conclude that given only one order of traversal of a tree it is possible to construct a number of binary trees, a unique binary tree is not possible to be constructed. For construction of a unique binary tree we require two orders in which one has to be inorder, the other can be preorder or postorder.

To draw a unique binary tree when inorder and preorder traversal of the tree is given :

(i) The root of T is obtained by choosing the first vertex in its preorder.
(ii) The left child of the root vertex is obtained as follows. First use the inroder traversal to find the vertices in the left subtree of the binary tree (all the vertices to the left of this vertex in the inorder traversal are the part of the left subtree). The left child of the root is obtained by selecting the first vertex in the preorder traversal of the left subtree draw the left child.
(iii) Use the inorder traversal to find the vertices in the right subtree of the binary tree (all the vertices to the right of the first vertex are the part of the right subtree).
Then the right child is obtained by selecting the first vertex in the preorder traversal of the right subtree. Draw the right child.
(iv) The procedure is repeated recursively until every vertex is not visited in preorder.

To draw a unique binary tree when inorder and postorder traversal of the tree is given :

(i) The root of the binary tree is obtained by choosing the last vertex in the postorder traversal.
(ii) The right child of the root vertex is obtained as follows. First use the inorder traversal to find the vertices in the right subtree. (all the vertices right to the root vertex in the inorder traversal are the vertices of the right subtree). The right child of the root is obtained by selecting the last vertex in the postorder traversal. Draw the right child.
(iii) Use the inorder traversal to find the vertices in the left subtree of the binary tree. Then the left child is obtained by selecting the last vertex in the postorder traversal of the left subtree. Draw the left child.
(iv) The process is repeated recursively until every vertex is not visited in postorder.

Representation of algebraic structure of binary trees
Binary trees are used to represent algebraic expressions, the vertices of the tree are labeled with the numbers, variables or operations that makeup the expression. The leaves of the tree can be labeled with numebrs or variables operations such as addition subtraction, multiplication, division or exponentiation can only be assigned to internal vertices. The operation at each vertex operates on its left and right subtrees from left to right.