Connected And Disconnected Graph

CONNECTED AND DISCONNECTED GRAPHS: A graph G is said to be a connected if every pair of vertices in G are connected. Otherwise, G is called a disconnected graph. Two vertices in G are said to be connected if there is at least one path from one vertex to the other.

In other words, a graph G is said to be connected if there is at least one path between every two vertices in G and disconnected if G has at least one pair of vertices between which there is no path. A graph is connected if we can reach any vertex from any other vertex by travelling along the edges and disconnected otherwise.
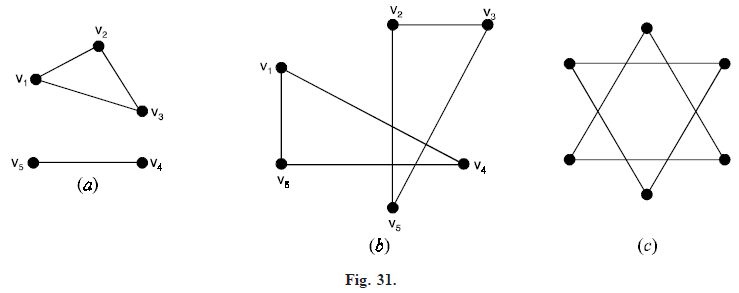
For example, the graphs in Figure 30(a, b, c, d, e) are connected whereas the graphs in Figure 31(a, b, c) are disconnected.

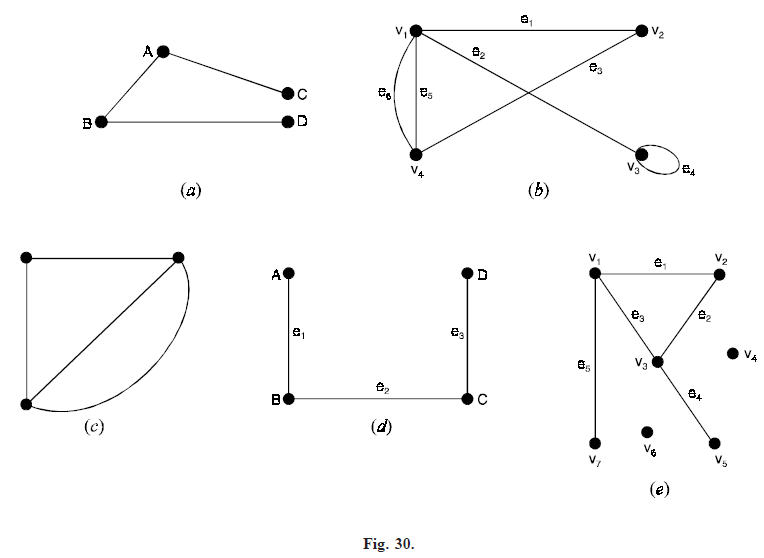
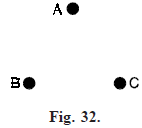
A complete graph is always connected, also, a null graph of more than one vertex is disconnected (see Fig. 32). All paths and circuits in a graph G are connected subgraphs of G.

Every graph G consists of one or more connected graphs, each such connected graph is a subgraph of G and is called a component of G. A connected graph has only one component and a disconnected graph has two or more components. For example, the graphs in Figure 31(a, b) have two components each.

Path graphs and cycle graphs: A connected graph that is 2-regular is called a cycle graph. Denote the cycle graph of n vertices by Γn. A circuit in a graph, if it exists, is a cycle subgraph of the graph. The graph obtained from Γn by removing an edge is called the path graph of n vertices, it is denoted by Pn.

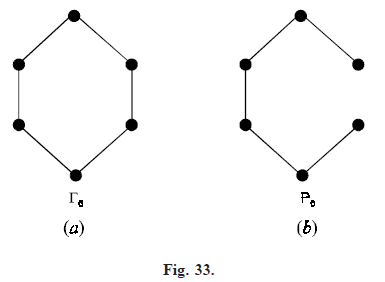
The graphs Γ6 and P6 are shown in Figure 33(a) and 33(b) respectively.

Rank and nullity: For a graph G with n vertices, m edges and k components we define the rank of G and is denoted
by ρ(G) and the nullity of G is denoted by μ(G) as follows.
ρ(G) = Rank of G = n – k
μ(G) = Nullity of G = m – ρ(G) = m – n k
If G is connected, then we have
ρ(G) = n – 1 and μ(G) = m – n 1.