Connected Digraphs

CONNECTED DIGRAPHS

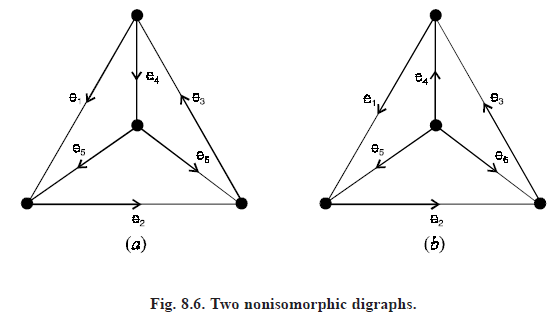
Strongly Connected: A digraph G is said to be strongly connected if there is atleast one directed path from every vertex to every other vertex.

Weakly Connected: A digraph G is said to be weakly connected if its corresponding undirected graph is connected
but G is not strongly connected.

Fig. 8.6, one of the digraphs is strongly connected, and the other one is weakly connected.

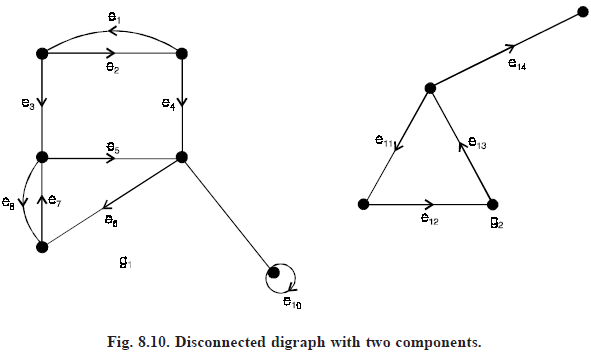
Component and Fragments: Each maximal connected (weakly or strongly) subgraph of a digraph G is called a component of G. But within each component of G the maximal strongly connected subgraphs are called the fragments (or strongly connected fragments) of G.

For example, the digraph in Fig. 10, consists of two components. The component g1 contains three fragments {e1, e2}, {e5, e6, e7, e8} and {e10}.

We observe that e3, e4 and e9 do not appear in any fragment of g1.