Counting Tree

COUNTING TREES
The subject of graph enumeration is concerned with the problem of finding out how many nonisomorphic graphs possess a given property. The subject was initiated in the 1850’s by Arthur Cayley, who later applied it to the problem of enumerating alkanes Cn H2n 2 with a given number of carbon atoms. This problem is that of counting the number of trees in which the degree of each vertex is either 4 or 1. Many standard problems of graph enumeration have been solved.

For example, it is possible to calculate the number of graphs, connected graphs, trees and Eulerian graphs with a given number of vertices and edges, corresponding general results for planar graphs and Hamiltonian graphs have, however, not yet been obtained. Most of the known results can be obtained by using a fundamental enumeration theorem due to Polya, a good account of which may be found in Harary and Palmer.

Unfortunately, in almost every case it is impossible to express these results by means of simple formulas. Consider Fig. (3.27), which shows three ways of labelling a tree with four vertices. Since the second labelled tree is the reverse of the first one, these two labelled trees are the same. On the other hand, neither is isomorphic to the third labelled tree, as you can see by comparing the degrees of vertex 3.

Thus, the reverse of any labelling does not result in a new one, and so the number of ways of
labelling this tree is
(4!) / 2 = 12.
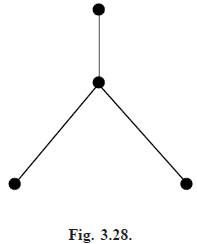
Similarly, the number of ways of labelling the tree in Fig. (3.28) is 4, since the central vertex can be labelled in four different ways, and each one determines the labelling. Thus, the total number of non-isomorphic labelled trees on four vertices is 12 4 = 16.

Theorem. Let T be a graph with n vertices. Then the following statements are equivalent :
(i) T is a tree
(ii) T contains no cycles, and has n – 1 edges
(iii) T is connected and has n – 1 edges
(iv) T is connected and each edge is a bridge
(v) Any two vertices of T are connected by exactly one path
(vi) T contains no cycles, but the addition of any new edge creates exactly one cycle.

Proof. If n = 1, all six results are trivial, we therefore assume that n ≥ 2.
(i) ⇒ (iii)
Since T contains no cycles, the removal of any edge must disconnect T into two graphs, each of which is a tree.
It follows by induction that the number of edges in each of these two trees is one fewer than the number of vertices. We deduce that the total number of edges of T is n – 1.
(ii) ⇒ (iii)
If T is disconnected, then each component of T is a connected graph with no cycles and hence, by the previous part, the number of vertices in each component exceeds the number of edges by 1. It follows that the total number of vertices of T exceeds the total number of edges by atleast 2, contradicting the fact that T has n – 1 edges.

(iii) ⇒ (iv)
The removal of any edge results in a graph with n vertices and n – 2 edges, which must be disconnected.
(iv) ⇒ (v)
Since T is connected, each pair of vertices is connected by atleast one path.
If a given pair of vertices is connected by two paths, then they enclose a cycle, contradicting the fact that each edge is a bridge.
(v) ⇒ (vi)
If T contained a cycle, then any two vertices in the cycle would be connected by atleast two paths, contradicting statement (v).
If an edge e is added to T, then, since the vertices incident with e are already connected in T, a cycle is created. The fact that only one cycle is obtained.
(vi) ⇒ (i)
Suppose that T is disconnected.
If we add to T any edge joining a vertex of one component to a vertex in another, then no cycle is created.

Corollary :
If G is a forest with n vertices and k components, then G has n – k edges.