Coverings

COVERINGS: A point and a line are said to cover each other if they are incident. A set of points which covers all the lines of a graph G is called a point cover for G, while a set of lines which covers all the points is a line cover.

Point covering number and line covering number
The smallest number of points in any point cover for G is called its point covering number and is denoted by α0 (G) or α0. Similarly α1 (G) or α1 is the smallest number of lines in any line cover of G and is called its line covering number.

For example. α0 (KP) = P – 1 and α (KP) = [(P 1)/2].
A point cover or line cover is called minimum if it contains α0 (respectively α1) dements.

We observe that a point cover may be minimum without being minimum, such a set of points is given by the 6 non cut points in Fig. 7.1(a) below. The same holds for line covers, the 6 lines incident with the cut point serve.

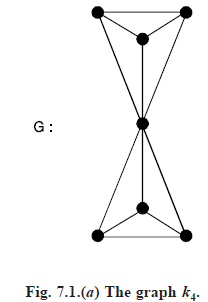
INDEPENDENCE: A set of points in G is independent if no two of them are adjacent.

Point independence number: The largest number of points in such a set is called the point is independence number of G and is denoted by β0 (G) or β0.

Line independence number: An independent set of lines of G has no two of its lines adjacent and the maximum cardinality of such a set is the line independence number β1 (G) or β1.

For the complete graph, β0 (KP) = 1 and β1 (KP) = [P/2].

From the above graph, β0 (G) = 2 and β1(G) = 3.