Cut Matrix
Cut Matrix: If all the cuts of a nontrivial and loopless graph G = (V,E) are I1, . . . , It, then the cut matrix of G is a t × m matrix Q = (qij), where m is the number of edges in G and
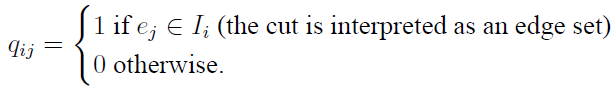
Example. For the graph
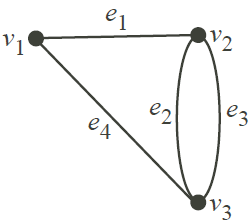
the cuts are I1 = {e1, e4}, I2 = {e2, e3, e4} and I3 = {e1, e2, e3}. The cut matrix is
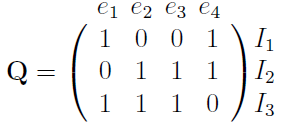
Remark. If the graph has n vertices, then it has 1/2 (2n − 2) = 2n−1 − 1 cuts. Usually, there are not this many distinct edge sets. For the cut matrix, we only take one cut corresponding to an edge set so that there would not be repeated rows. Even so, there are usually too many rows. If G is a nontrivial and loopless digraph, then we assign an arbitrary direction to every cut (V1, V2) the orientation of (V1, V2) is from V1 to V2. In other words, we consider oriented cuts and we pick only one direction from the two possibilities. Then, the cut matrix Q = (qij) is

Example. For the digraph
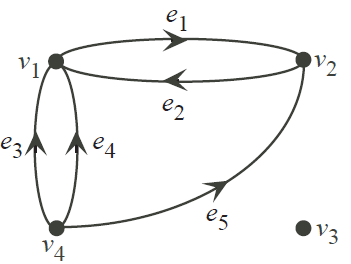
the different cuts (interpreted as edge sets) are I1 = {e1, e2, e3, e4} (in the direction of e1), I2 = {e3, e4, e5} (in the direction of e3), I3 = {e1, e2, e5} (in the direction of e1) and I4 = ∅. The cut matrix is
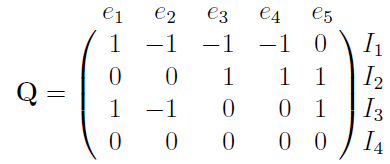
Since h{v}, V − {v}i is a cut for every vertex v, rows of the all-vertex incidence matrix are rows of Q. If we are dealing with directed graphs, then these rows may have to be multiplied by −1.