Dijkstra Algorithm
DIJKSTRA’S ALGORITHM: To find a shortest path from vertex A to vertex E in a weighted graph, carry out the following procedure.
Step 1 : Assign to A the label (–, 0).
Step 2 : Until E is labeled or no further labels can be assigned, do the following
(i) For each labeled vertex u(x, d) and for each unlabeled vertex v adjacent to u, compute d w(e), where e = uv.
(ii) For each labeled vertex u and adjacent unlabeled vertex v giving minimum d′ = d w(e), assign to v the label (u, d′). If a vertex can be labeled (x, d′) for various vertices x, make any choice.
Dijkstra’s algorithm (Improved): To find the length of a shortest path from vertex A to vertex E in a weighted graph, proceed as follows:
Step 1 : Set v1 = A and assign to this vertex the permanent label O. Assign every other vertex a temporary label of ∞, where ∞ is a symbol which, by definition, is deemed to be larger than any real number.
Step 2 : Until E has been assigned a permanent label or no temporary labels are changed in (a) or (b), do the following.
(a) Take the vertex vi which most recently acquired a permanent label, say d. For each vertex v which is adjacent to vi and has not yet received a permanent label, if d w(viv) < t the current temporary label of v to d w(viv).
(b) Take a vertex v which has a temporary smallest among all temporary labels in the graph.
Set vi 1 = v and make its temporary label permanent. If there are several vertices v which tie for smallest temporary label, make any choice.
Floyd-Warshall algorithm: To find the shortest distances between all pairs of vertices in a weighted graph where the vertices are v1, v2, ......, vn, carry out the following procedure:
Step 1 : For i = 1 to n, set d(i, i) = 0,
For i ≠ j, if vivj is an edge, let d(i, j) be the weight of this edge; otherwise
Set d(i, j) = ∞.
Step 2 : For k = 1 to n,
for i, j = 1 to n,
let d(i, j) = min {d(i, j), d(i, k) d(k, j)}
The final value of d(i, j) is the shortest distance from vi to vj.
Problem . Apply Dijkstra’s algorithm to the graph given below and find the shortest path from a to f.
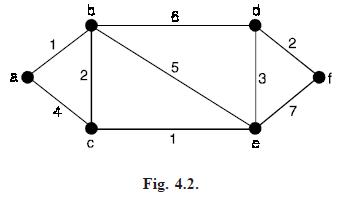
Solution. The initial labelling is given by

Iteration 1 : u = a has L(u) = 0. T becomes T–{a}. There are two edges incident a, i.e., ab and ac where b and CET.
L(b) = min {old L(b), L(a) w(ab)} = min {α, 0 1.0} = 1.0
L(c) = min {old L(c), L(a) w(ac)} = min {α, 0 4.0} = 4.0
Hence minimum label is L(b) = 1.0
