Directed And Undirected Graph

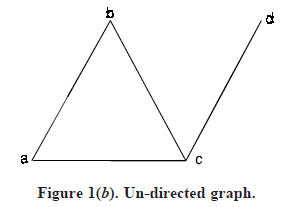
Directed graph: A directed graph or digraph G consists of a set V of vertices and a set E of edges such that e ∈ E is associated with an ordered pair of vertices. In other words, if each edge of the graph G has a direction then the graph is called directed graph.

In the diagram of directed graph, each edge e = (u, v) is represented by an arrow or directed curve from initial point u of e to the terminal point v. Figure 1(a) is an example of a directed graph.

Suppose e = (u, v) is a directed edge in a digraph, then

1. u is called the initial vertex of e and v is the terminal vertex of e
2. e is said to be incident from u and to be incident to v.
3. u is adjacent to v, and v is adjacent from u.

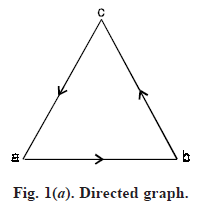
Un-directed graph: An un-directed graph G consists of set V of vertices and a set E of edges such that each edge e ∈ E is associated with an unordered pair of vertices. In other words, if each edge of the graph G has no direction then the graph is called un-directed graph.

Figure 1(b) is an example of an undirected graph. We can refer to an edge joining the vertex pair i and j as either (i, j) or (j, i).