Edges And Vertex

PARALLEL EDGES: Two (directed) edges e and e′ of a digraph D are said to be parallel if e and e′ have the same initial vertex and the same terminal vertex.
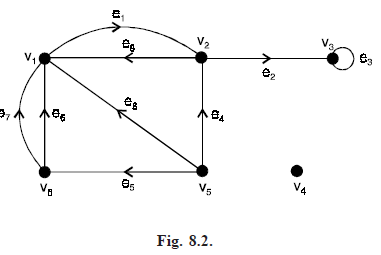
In the digraph in Fig. 8.2 the edges e6 and e7 are parallel edges whereas the edges e1 and e9 are not parallel. e1 and e6 are parallel edges in the underlying graph.

INCIDENCE: In a digraph every edge has two end vertices, one vertex from which it begins and the other vertex at which it terminates. If an edge e begins at a vertex u and terminates at a vertex v, we say that e is incident out of u and incident into v. Here, u is called the initial vertex and v is called the terminal vertex of e.
For example, in the digraph in Fig. 8.2, the edge e1 is incident out of the vertex v1 and incident into the vertex v2, v1 is the initial vertex and v2 is the terminal vertex of the edge e1. For a self-loop in a digraph, the initial and terminal vertices are one and the same. In Fig. 8.2 the edge e3 is a self-loop with v3 as the initial and terminal vertex.

IN-DEGREE AND OUT-DEGREE: If v is a vertex of a digraph D, the number of edges incident out of v is called the out-degree of v and the number of edges incident into v is called the in-degree of v. The out-degree of v is denoted by d (v) and the in-degree of v is denoted by d–(v).
For example, the out-degrees and in-degrees of the six vertices of the digraph shown in Fig. 8.2. are as given below :

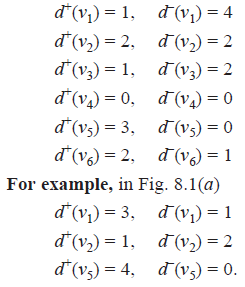
ISOLATED VERTEX: If v is a vertex of a digraph D then v is called an isolated vertex of D if d (v) = d–(v) = 0.

PENDANT VERTEX: If v is a vertex of a digraph D then v is called a pendant vertex of D if d (v) d–(v) = 1.

SOURCE: If v is a vertex of a digraph D then v is called a source of D if d–(v) = 0.

SINK: If v is a vertex of a digraph D then v is called a sink of D if d (v) = 0. The digraph is Fig. 8.1(a) has v4 as an isolated vertex and v5 as a source. In the digraph in Fig. 8.1(a), the vertices B and C are pendant vertices, C is a source and B is a sink.