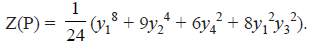Equivalance Classes Of Function
EQUIVALENCE CLASSES OF FUNCTIONS: Consider two sets D and R, with the number of elements | D | and | R | respectively. Let f be a mapping or function which maps each element d from doamin D to a unique image f(d) in range R. Since each of the | D | elements can be mapped into any of | R | elements, the number of different functions from D to R is | R || D |.
Let there be a permutation group P on the elements of set D. Then define two mappings f1 and f2 as P-equivalent if there is some permutation π in P such that for every d in D we have
f1(d) = f2[π(d)] ...(1)
The relationship defined by (1) is an equivalence relation can be shown as follows :
(i) Since P is a permutation group, it contains the identity permutation and thus (1) is reflexive.
(ii) If P contains permutation π, it also contains the inverse permutation π– 1. Therefore, the relation is symmetric also.
(iii) Furthermore, if P contains permutations π1 and π2, it must also contain the permutation π1π2. This makes P-equivalence a transitive relation.
The permutation group P on D is the set of all those permutations that can be produced by rotations of the cube.
These permutations with their cycle structures are :
(i) One identity permutation. Its cycle structure is y1 8.
(ii) Three 180° rotations around lines connecting the centers of opposite faces. Its cycles structure is y24.
(iii) Six 90° rotations (clockwise and counter clockwise) around lines connecting the centers of opposite faces. The cycle structure is y42.
(iv) Six 180° rotations around lines connecting the mid-points of opposite edges. The corresponding cycle structure is y24.
(v) Eight 120° rotations around lines connecting opposite corners in the cube. The cycle structure of the corresponding permutation is y12.y33.
The cycle index of this group consisting of these 24 permutations is, therefore,