Euler's Theorem

EULER’S FORMULA: The basic results about planar graph known as Euler’s formula is the basic computational tools for planar graph.
Theorem . Euler’s Formula: If a connected planar graph G has n vertices, e edges and r region, then n – e r = 2.

Proof. We prove the theorem by induction on e, number of edges of G.

Basis of induction : If e = 0 then G must have just one vertex. i.e., n = 1 and one infinite region, i.e., r = 1
Then n – e r = 1 – 0 1 = 2.
If e = 1 (though it is not necessary), then the number of vertices of G is either 1 or 2, the first possibility of occurring when the edge is a loop. These two possibilities give rise to two regions and one region respectively, as shown in Figure (2.17) below.

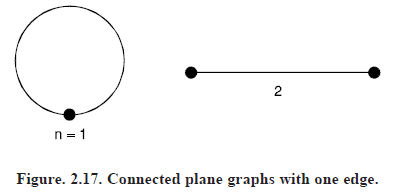
In the case of loop, n – e r = 1 – 1 2 = 2 and in case of non-loop, n – e r = 2 – 1 1 = 2. Hence the result is true.

Induction hypothesis : Now, we suppose that the result is true for any connected plane graph G with e – 1 edges.

Induction step : We add one new edge K to G to form a connected supergraph of G which is denoted by G K. There are following three possibilities.

(i) K is a loop, in which case a new region bounded by the loop is created but the number of vertices remains unchanged.
(ii) K joins two distinct vertices of G, in which case one of the region of G is split into two, so that number of regions is increased by 1, but the number of vertices remains unchanged.
(iii) K is incident with only one vertex of G on which case another vertex must be added, increasing the number of vertices by one, but leaving the number of regions unchanged.

If let n′, e′ and r′ denote the number of vertices, edges and regions in G and n, e and r denote the same in G K. Then

In case (i) n – e r = n′ – (e′ 1) (r′ 1) = n′ – e′ r′.
In case (ii) n – e r = n′ – (e′ 1) (r′ 1) = n′ – e′ r′
In case (iii) n – e r = (n′ 1) – (e′ 1) r′ = n′ – e′ r′.

But by our induction hypothesis, n′ – e′ r′ = 2. Thus in each case n – e r = 2.

Now any plane connected graph with e edges is of the form G K, for some connected graph G with e – 1 edges and a new edge K.
Hence by mathematical induction the formula is true for all plane graphs.

Corollary (1)
If a plane graph has K components then n – e r = K 1. The result follows on applying Euler’s formula to each component separately, remembering not to count the infinite region more than once.

Corollary (2)
If G is connected simple planar graph with n (≥ 3) vertices and e edges, then e ≤ 3n – 6.
Proof. Each region is bounded by atleast three edges (since the graphs discussed here are simple graphs, no multiple edges that could produce regions of degree 2 or loops that could produce regions of degree 1, are permitted) and edges belong to exactly two regions.
2e ≥ 3r
If we combine this with Euler’s formula, n – e r = 2, we get 3r = 6 – 3n 3e ≤ 2e which is equivalent to e ≤ 3n – 6.

Corollary (3)
If G is connected simple planar graph with n (≥ 3) vertices and e edges and no circuits of length 3, then e ≤ 2n – 4.
Proof. If the graph is planar, then the degree of each region is atleast 4. Hence the total number of edges around all the regions is atleast 4r. Since every edge borders two regions, the total number of edges around all the regions is 2e, so we established that 2e ≥ 4r, which is equivalent to 2r ≤ e. If we combine this with

Euler’s formula n – e r = 2, we get

2r = 4 – 2n 2e ≤ e

which is equivalent to e ≤ 2n – 4.