Eulerial Graphs

EULERIAN GRAPHS

Euler path: A path in a graph G is called Euler path if it includes every edges exactly once. Since the path contains every edge exactly once, it is also called Euler trail.

Euler circuit: An Euler path that is circuit is called Euler circuit. A graph which has a Eulerian circuit is called an Eulerian graph.

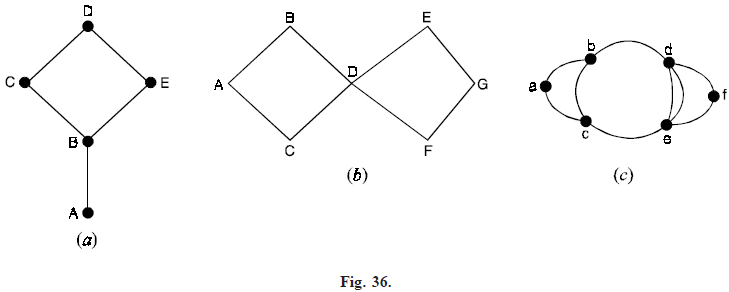
The graph of Figure 36(a) has an Euler path but no Euler circuit. Note that two vertices A and B are of odd degrees 1 and 3 respectively. That means AB can be used to either arrive at vertex A or leave vertex A but not for both. Thus an Euler path can be found if we start either from vertex A or from B. ABCDEB and BCDEBA are two Euler paths. Starting from any vertex no Euler circuit can be found.

The graph of Figure 36(b) has both Euler circuit and Euler path. ABDEGFDCA is an Euler path and circuit. Note that all vertices of even degree. No Euler path and circuit is possible in Figure 36(c). Note that all vertices are not even degree and more than two vertices are of odd degree. The existence of Euler path and circuit depends on the degree of vertices.

Note : To determine whether a graph G has an Euler circuit, we note the following points :
(i) List the degree of all vertices in the graph.
(ii) If any value is zero, the graph is not connected and hence it cannot have Euler path or Euler circuit.
(iii) If all the degrees are even, then G has both Euler path and Euler circuit.
(iv) If exactly two vertices are odd degree, then G has Euler path but no Euler circuit.

Theorem. The following statements are equivalent for a connected graph G :
(i) G is Eulerian
(ii) Every point of G has even degree
(iii) The set of lines of G be partitioned into cycles.
Proof. (i) implies (ii)
Let T be an Eulerian trail in G.

Each occurrence of a given point in T contributes 2 to the degree of that point, and since each line of G appears exactly once in T, every point must have even degree. (ii) implies (iii)

Since G is connected and non trivial, every point has degree at least 2, so G contains a cycle Z. The removal of the lines of Z results in a spanning subgraph G1 in which every point still has even degree. If G1 has no lines, then (iii) already holds ; otherwise, repetition of the argument applied to G1 results in a graph G2 in which again all points are even, etc. When a totally disconnected graph Gn is obtained, we have a partition of the lines of G into n cycles. (iii) implies (i)

Let Z1 be one of the cycles of this partition. If G consists only of this cycle, then G is obviously Eulerian. Otherwise, there is another cycle Z2 with a point v in common with Z1.

The walk beginning at v and consisting of the cycles Z1 and Z2 in succession is a closed trail containing the lines of these two cycles. By continuing this process, we can construct a closed trail containing all lines of G. Hence G is Eulerian.

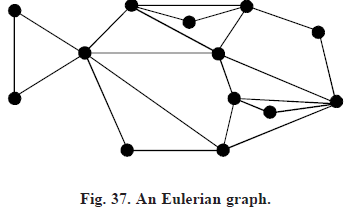
For example, the connected graph of Figure 37 in which every point has even degree has an Eulerian trail, and the set of lines can be partitioned into cycles.
Corollary (1) : Let G be a connected graph with exactly 2n odd points, n ≥ 1, then the set of lines of G can be
partitioned into n open trails.
Corollary (2) : Let G be a connected graph with exactly two odd points. Then G has an open trail containing all
the points and lines of G (which begins at one of the odd points and ends at the other).